Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Hayman, W. K.
and
Rippon, P. J.
2015.
Obituary: James (Jim) Gourlay Clunie 1926-2013.
Bulletin of the London Mathematical Society,
Vol. 47,
Issue. 3,
p.
533.


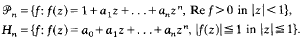
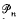 if and only if Re
if and only if Re 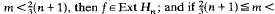 2
2