Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-25T02:55:54.705Z Has data issue: false hasContentIssue false
  • English
  • Français

Exit radii of submanifolds from cylindrical domains in warped product manifolds

Published online by Cambridge University Press:  03 June 2015

Hironori Kumura
Hironori Kumura*
Affiliation:
Department of Mathematics, Shizuoka University, Shizuoka 422-8529, Japan, ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Let UB(p0; ρ1) × f MV be a cylindrically bounded domain in a warped product manifold 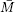:= MB × fMV and let M be an isometrically immersed submanifold in 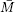. The purpose of this paper is to provide explicit radii of the geodesic balls of M which first exit from UB(p0; ρ1) × fMV for the case in which the mean curvature of M is sufficiently small and the lower bound of the Ricci curvature of M does not diverge to –∞ too rapidly at infinity.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 145 , Issue 3 , June 2015 , pp. 559 - 569
Copyright
Copyright © Royal Society of Edinburgh 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1 Alías, L. J., Bessa, G. P., Montenegro, J. F. and Piccione, P.. Curvature estimates for submanifolds in warped products. Preprint, 2010. (Available at http://arxiv.org/abs/1009.3467.)Google Scholar
2 Collin, P. and Rosenberg, H.. Notes sur la démonstration de Nadirashvili des conjectures de Hadamard et Calabi–Yau. Bull. Sci. Math. 123 (1999), 563–575.Google Scholar
3 Jorge, L. and Koutroufiotis, D.. An estimate for the curvature of bounded submanifolds. Am. J. Math. 103 (1981), 711–725.Google Scholar
4 Jorge, L. and Xavier, F.. An inequality between the exterior diameter and the mean curvature of bounded immersion. Math. Z. 178 (1981), 77–82.Google Scholar
5 Kasue, A.. Applications of Laplacian and Hessian comparison theorems. In Geometry of Geodesics and Related Topics: Proc. Symp., University of Tokyo, November 29-December 3, 1982. Advanced Studies in Pure Mathematics, vol. 3, pp. 333–386 (Elsevier, 1984).Google Scholar
6 Kasue, A.. Estimates for solutions of Poisson equations and their application to submanifolds. Lecture Notes in Mathematics, vol. 1090, pp. 1–14 (Springer, 1984).Google Scholar
7 Martín, F. and Morales, S.. A complete bounded minimal cylinder in ℝ3 . Michigan Math. J. 47 (2000), 499–514.Google Scholar
8 Nadirashvili, N. S.. Hadamard’s and Calabi–Yau conjectures on negatively curved and minimal surfaces. Invent. Math. 126 (1996), 457–465.Google Scholar
9 Omori, H.. Isometric immersions of Riemannian manifolds. J. Math. Soc. Jpn 19 (1967), 205–214.Google Scholar
10 Zhou, D.. Laplace inequalities with geometric applications. Arch. Math. 67 (1996), 50–58.Google Scholar