Published online by Cambridge University Press: 14 November 2011
Weakly coupled semilinear elliptic systems of the form
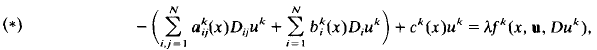
are considered in RN, N≧2, where k = 1, 2, …, M, u = (u1, …, uM) and λ is a real constant. The aim of this paper is to give sufficient conditions for (*) to have entire solutions whose components are positive in RN and converge to non-negative constants as |x| tends to ∞. For this purpose a new supersolution-subsolution method is developed for the system (*) without any hypotheses on the monotonicity of the non-linear terms fk with respect to u.