No CrossRef data available.
Published online by Cambridge University Press: 14 November 2011
For an unbounded self-adjoint operator A in a separable Hilbert space ℌ and scalar real-valued functions a(t), q(t), r(t), t ∊ ℝ, consider the differential expression
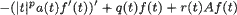
acting on ℌ-valued functions f(t), t ∊ ℝ, and degenerating at t = 0. Let Sp denotethe corresponding minimal symmetric operator in the Hilbert space  (ℝ) of ℌ-valued functions f(t) with ℌ-norm ∥f(t)∥ square integrable on the line. The infiniteness of the deficiency indices of Sp, 1/2 < p < 3/2, is proved under natural restrictions on a(t), r(t), q(t). The conditions implying their equality to 0 for p ≥ 3/2 are given. In the case of a self-adjoint differential operator A acting in ℌ = L2(ℝn), the first of these results implies examples of symmetric degenerate differential operators with infinite deficiency indices in L2(ℝm), m = n + 1.
(ℝ) of ℌ-valued functions f(t) with ℌ-norm ∥f(t)∥ square integrable on the line. The infiniteness of the deficiency indices of Sp, 1/2 < p < 3/2, is proved under natural restrictions on a(t), r(t), q(t). The conditions implying their equality to 0 for p ≥ 3/2 are given. In the case of a self-adjoint differential operator A acting in ℌ = L2(ℝn), the first of these results implies examples of symmetric degenerate differential operators with infinite deficiency indices in L2(ℝm), m = n + 1.