We consider a non-homogeneous generalized Burgers equation

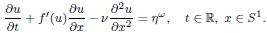
Here, ν is small and positive, f is strongly convex and satisfies a growth assumption, while ηω is a space-smooth random ‘kicked’ forcing term. For any solution u of this equation, we consider the quasi-stationary regime, corresponding to t ⩾ 2. After taking the ensemble average, we obtain upper estimates and time-averaged lower estimates for a class of Sobolev norms of u. These estimates are of the form Cν-β with the same values of β for bounds from above and from below. They depend on η and f, but do not depend on the time t or the initial condition.