Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Milatovic, Ognjen
2017.
Self‐adjointness of perturbed biharmonic operators on Riemannian manifolds.
Mathematische Nachrichten,
Vol. 290,
Issue. 17-18,
p.
2948.
Milatovic, Ognjen
2018.
Self-Adjointness, $$\varvec{m}$$ m -Accretivity, and Separability for Perturbations of Laplacian and Bi-Laplacian on Riemannian Manifolds.
Integral Equations and Operator Theory,
Vol. 90,
Issue. 2,
Milatovic, Ognjen
and
Saratchandran, Hemanth
2019.
Inequalities and separation for covariant Schrödinger operators.
Journal of Geometry and Physics,
Vol. 138,
Issue. ,
p.
215.
Saratchandran, Hemanth
2021.
Essential self‐adjointness of perturbed quadharmonic operators on Riemannian manifolds with an application to the separation problem.
Mathematische Nachrichten,
Vol. 294,
Issue. 5,
p.
997.
Milatovic, Ognjen
and
Saratchandran, Hemanth
2022.
Essential Self-Adjointness of Perturbed Biharmonic Operators via Conformally Transformed Metrics.
Potential Analysis,
Vol. 56,
Issue. 4,
p.
623.
ATİA, Hany
and
EMAM, Hala H.
2022.
Essential self-adjointness for covariant tri-harmonic operators on manifolds and the separation problem.
Hacettepe Journal of Mathematics and Statistics,
Vol. 51,
Issue. 5,
p.
1321.
Ellouz, Hanen
Feki, Ines
and
Jeribi, Aref
2022.
On the closedness and self-adjointness of 3×3 operator matrices and application to a non-relativistic three-channel potential scattering model.
Asymptotic Analysis,
Vol. 130,
Issue. 3-4,
p.
409.


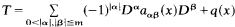 , on
, on  , and self-adjoint on
, and self-adjoint on 