No CrossRef data available.
Published online by Cambridge University Press: 14 November 2011
Let R1(x),…, Rd(x) be rational functions in Iℚ(x), such that 1, R1(x),…, Rd(x) are linearly independent over Iℚ. For almost all primes p, their mod p reductions, 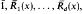 are well-defined rational functions over Fp and are linearly independent over Fp We show that asymptotically the points
are well-defined rational functions over Fp and are linearly independent over Fp We show that asymptotically the points
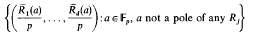
are uniformly distributed in [0, l)d.