Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-16T19:20:08.792Z Has data issue: false hasContentIssue false
  • English
  • Français

Embeddings of homogeneous Sobolev spaces on the entire space

Part of: Special classes of linear operators Linear function spaces and their duals Inequalities

Published online by Cambridge University Press:  09 March 2020

Zdeněk Mihula Open the ORCID record for Zdeněk Mihula [Opens in a new window]
Zdeněk Mihula*
Affiliation:
Faculty of Mathematics and Physics, Department of Mathematical Analysis, Charles University, Sokolovská 83, 186 75 Praha 8, Czech Republic
*
[email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We completely characterize the validity of the inequality 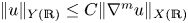$\| u \|_{Y(\mathbb R)} \leq C \| \nabla^{m} u \|_{X(\mathbb R)}$, where X and Y are rearrangement-invariant spaces, by reducing it to a considerably simpler one-dimensional inequality. Furthermore, we fully describe the optimal rearrangement-invariant space on either side of the inequality when the space on the other side is fixed. We also solve the same problem within the environment in which the competing spaces are Orlicz spaces. A variety of examples involving customary function spaces suitable for applications is also provided.

Keywords

Optimal function spacesRearrangement-invariant spacesReduction principleSobolev spaces

MSC classification

Primary: 26D10: Inequalities involving derivatives and differential and integral operators
Secondary: 46E30: Spaces of measurable functions ($L^p$-spaces, Orlicz spaces, Köthe function spaces, Lorentz spaces, rearrangement invariant spaces, ideal spaces, etc.) 46E35: Sobolev spaces and other spaces of “smooth” functions, embedding theorems, trace theorems 47B38: Operators on function spaces (general)
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 151 , Issue 1 , February 2021 , pp. 296 - 328
Check for updates
Copyright
Copyright © The Author(s), 2020. Published by The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Acerbi, E. and Mingione, G.. Regularity results for a class of functionals with non-standard growth. Arch. Ration. Mech. Anal. 156 (2001), 121–140. ISSN . https://doi.org/10.1007/s002050100117.CrossRefGoogle Scholar
2Adams, R. A. and Fournier, J. J. F.. Sobolev spaces, volume 140 of Pure and Applied Mathematics (Amsterdam) (Amsterdam: Elsevier/Academic Press, 2003), 2nd ed. ISBN 0-12-044143-8.Google Scholar
3Alberico, A., Cianchi, A., Pick, L. and Slavíková, L.. Sharp Sobolev type embeddings on the entire Euclidean space. Commun. Pure Appl. Anal. 17 (2018), 2011–2037. ISSN . https://doi.org/10.3934/cpaa.2018096.CrossRefGoogle Scholar
4Alves, C. O., Figueiredo, G. M. and Santos, J. A.. Strauss and Lions type results for a class of Orlicz–Sobolev spaces and applications. Topol. Methods Nonlinear Anal. 44 (2014), 435–456. ISSN . https://doi.org/10.12775/TMNA.2014.055.CrossRefGoogle Scholar
5Benkirane, A. and Elmahi, A.. An existence theorem for a strongly nonlinear elliptic problem in Orlicz spaces. Nonlinear Anal. 36 (1999), 11–24. ISSN . https://doi.org/10.1016/S0362-546X(97)00612-3.CrossRefGoogle Scholar
6Bennett, C. and Sharpley, R., Interpolation of operators, volume 129 of Pure and Applied Mathematics (Boston, MA: Academic Press, Inc., 1988). ISBN 0-12-088730-4.Google Scholar
7Berezhnoĭ, E. I.. Sharp estimates for operators on cones in ideal spaces. Trudy Mat. Inst. Steklov. 204 (1993), 3–34. ISSN . English translation in Proc. Steklov Inst. Math. 204 (1994), 1–25.Google Scholar
8Boyd, D. W.. The Hilbert transform on rearrangement-invariant spaces. Can. J. Math. 19 (1967), 599–616. ISSN . https://doi.org/10.4153/CJM-1967-053-7.CrossRefGoogle Scholar
9Boyd, D. W.. Indices for the Orlicz spaces. Pac. J. Math. 38 (1971), 315–323. ISSN . http://projecteuclid.org/euclid.pjm/1102970044.CrossRefGoogle Scholar
10Brézis, H. and Wainger, S.. A note on limiting cases of Sobolev embeddings and convolution inequalities. Commun. Part. Differ. Equ. 5 (1980), 773–789. ISSN . https://doi.org/10.1080/03605308008820154.CrossRefGoogle Scholar
11Brudnyĭ, Ju.A.. Rational approximation and imbedding theorems. Dokl. Akad. Nauk SSSR 247 (1979), 269–272. ISSN . English translation in Soviet Math. Dokl. 20 (1979), 681–684.Google Scholar
12Cianchi, A.. Optimal Orlicz–Sobolev embeddings. Rev. Mat. Iberoamericana 20 (2004), 427–474. ISSN . https://doi.org/10.4171/RMI/396.CrossRefGoogle Scholar
13Cianchi, A. and Musil, V.. Optimal domain spaces in Orlicz–Sobolev embeddings. Indiana Univ. Math. J. 68 (2019), 925–966. ISSN . https://doi.org/10.1512/iumj.2019.68.7649.CrossRefGoogle Scholar
14Cianchi, A. and Pick, L.. Sobolev embeddings into BMO, VMO, and $L^\infty $. Ark. Mat. 36 (1998), 317–340. ISSN . https://doi.org/10.1007/BF02384772.CrossRefGoogle Scholar
15Cianchi, A. and Pick, L.. Optimal Sobolev trace embeddings. Trans. Am. Math. Soc. 368 (2016), 8349–8382. ISSN . https://doi.org/10.1090/tran/6606.CrossRefGoogle Scholar
16Cianchi, A., Pick, L. and Slavíková, L.. Higher-order Sobolev embeddings and isoperimetric inequalities. Adv. Math. 273 (2015), 568–650. ISSN . https://doi.org/10.1016/j.aim.2014.12.027.CrossRefGoogle Scholar
17Cwikel, M. and Pustylnik, E.. Weak type interpolation near ‘endpoint’ spaces. J. Funct. Anal. 171 (2000), 235–277. ISSN . https://doi.org/10.1006/jfan.1999.3502.CrossRefGoogle Scholar
18Donaldson, T.. Nonlinear elliptic boundary value problems in Orlicz–Sobolev spaces. J. Differ. Equ. 10 (1971), 507–528. ISSN . https://doi.org/10.1016/0022-0396(71)90009-X.CrossRefGoogle Scholar
19Edmunds, D. E., Gurka, P. and Pick, L.. Compactness of Hardy-type integral operators in weighted Banach function spaces. Studia Math. 109 (1994), 73–90. ISSN . http://eudml.org/doc/216062.Google Scholar
20Edmunds, D. E., Kerman, R. and Pick, L.. Optimal Sobolev imbeddings involving rearrangement-invariant quasinorms. J. Funct. Anal. 170 (2000), 307–355. ISSN . https://doi.org/10.1006/jfan.1999.3508.CrossRefGoogle Scholar
21Edmunds, D. E., Mihula, Z., Musil, V. and Pick, L.. Boundedness of classical operators on rearrangement-invariant spaces. J. Funct. Anal. 278 (2020), 108341. ISSN . https://doi.org/10.1016/j.jfa.2019.108341.CrossRefGoogle Scholar
22Evans, W. D., Opic, B. and Pick, L.. Interpolation of operators on scales of generalized Lorentz–Zygmund spaces. Math. Nachr. 182 (1996), 127–181. ISSN . https://doi.org/10.1002/mana.19961820108.CrossRefGoogle Scholar
23Evans, W. D., Opic, B. and Pick, L.. Real interpolation with logarithmic functors. J. Inequal. Appl. 7 (2002), 187–269. ISSN . https://doi.org/10.1155/S1025583402000127.Google Scholar
24Gagliardo, E.. Proprietà di alcune classi di funzioni in più variabili. Ricerche Mat. 7 (1958), 102–137. ISSN .Google Scholar
25Gogatishvili, A., Opic, B. and Pick, L.. Weighted inequalities for Hardy-type operators involving suprema. Collect. Math. 57 (2006), 227–255. ISSN . https://eudml.org/doc/41777.Google Scholar
26Hansson, K.. Imbedding theorems of Sobolev type in potential theory. Math. Scand. 45 (1979), 77–102. ISSN . https://doi.org/10.7146/math.scand.a-11827.CrossRefGoogle Scholar
27Kerman, R. and Pick, L.. Optimal Sobolev imbeddings. Forum Math. 18 (2006), 535–570. ISSN . https://doi.org/10.1515/FORUM.2006.028.CrossRefGoogle Scholar
28Krasnosel'skiĭ, M. A. and Rutickiĭ, Ja. B.. Convex functions and Orlicz spaces. Translated from the first Russian edition by Leo F. Boron. P. Noordhoff Ltd., Groningen, 1961.Google Scholar
29Lieb, E. H. and Loss, M.. Analysis, volume 14 of Graduate Studies in Mathematics (Providence, RI: American Mathematical Society, 2001), 2nd ed. ISBN 978-0-8218-2783-3. https://doi.org/10.1090/gsm/014.Google Scholar
30Maz'ya, V. G.. Sobolev spaces with applications to elliptic partial differential equations, volume 342 of Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences] (Heidelberg: Springer, 2011). ISBN 978-3-642-15563-5. https://doi.org/10.1007/978-3-642-15564-2.Google Scholar
31Musil, V.. Classical operators of harmonic analysis in Orlicz spaces, Ph.D. Thesis. Charles University, Faculty of Mathematics and Physics, 2018. https://is.cuni.cz/webapps/zzp/detail/150069/.Google Scholar
32Musil, V.. Fractional maximal operator in Orlicz spaces. J. Math. Anal. Appl. 474 (2019), 94–115. ISSN . https://doi.org/10.1016/j.jmaa.2019.01.034.CrossRefGoogle Scholar
33Musil, V. and Ol'hava, R.. Interpolation theorem for Marcinkiewicz spaces with applications to Lorentz gamma spaces. Math. Nachr. 292 (2019), 1106–1121. ISSN . https://doi.org/10.1002/mana.201700452.CrossRefGoogle Scholar
34Nirenberg, L.. On elliptic partial differential equations. Ann. Scuola Norm. Sup. Pisa (3) 13 (1959), 115–162. http://www.numdam.org/item/ASNSP_1959_3_13_2_115_0.Google Scholar
35O'Neil, R.. Convolution operators and $L(p,q)$ spaces. Duke Math. J. 30 (1963), 129–142. ISSN . http://projecteuclid.org/euclid.dmj/1077374532.CrossRefGoogle Scholar
36Opic, B. and Pick, L.. On generalized Lorentz–Zygmund spaces. Math. Inequal. Appl. 2 (1999), 391–467. ISSN . https://doi.org/10.7153/mia-02-35.Google Scholar
37Peetre, J.. Espaces d'interpolation et théorème de Soboleff. Ann. Inst. Fourier (Grenoble) 16 (1966), 279–317. ISSN . https://doi.org/10.5802/aif.232.CrossRefGoogle Scholar
38Peša, D.. Reduction principle for a certain class of kernel-type operators. Accepted for publication in Math. Nachr. arXiv:1908.06313 [math.FA].Google Scholar
39Pick, L., Kufner, A., John, O. and Fučík, S.. Function spaces. Vol. 1, volume 14 of De Gruyter Series in Nonlinear Analysis and Applications (Berlin: Walter de Gruyter & Co., 2013), extended edition. ISBN 978-3-11-025041-1; 978-3-11-025042-8.Google Scholar
40Rao, M. M. and Ren, Z. D.. Theory of Orlicz spaces, volume 146 of Monographs and Textbooks in Pure and Applied Mathematics (New York: Marcel Dekker, Inc., 1991). ISBN 0-8247-8478-2.Google Scholar
41Sobolev, S. L.. On a theorem of functional analysis. Mat. Sb. 46 (1938), 471–496.Google Scholar
42Sobolev, S. L.. Some applications of functional analysis in mathematical physics, volume 90 of Translations of Mathematical Monographs (Providence, RI: American Mathematical Society, 1991). ISBN 0-8218-4549-7.Google Scholar
43Trudinger, N. S.. On imbeddings into Orlicz spaces and some applications. J. Math. Mech. 17 (1967), 473–483. https://www.jstor.org/stable/24901677.Google Scholar
44Vuillermot, P.-A.. A class of Orlicz–Sobolev spaces with applications to variational problems involving nonlinear Hill's equations. J. Math. Anal. Appl. 89 (1982), 327–349. ISSN . https://doi.org/10.1016/0022-247X(82)90105-6.CrossRefGoogle Scholar
45Vybíral, J.. Optimal Sobolev embeddings on $\mathbb {R}^n$. Publ. Mat. 51 (2007), 17–44. ISSN . https://doi.org/10.5565/PUBLMAT_51107_02.CrossRefGoogle Scholar
46Zhikov, V. V.. Averaging of functionals of the calculus of variations and elasticity theory. Izv. Akad. Nauk SSSR Ser. Mat. 50 (1986), 675–710. 877, ISSN . https://doi.org/10.1070/im1987v029n01abeh000958.Google Scholar
47Ziemer, W. P.. Weakly differentiable functions: Sobolev spaces and functions of bounded variation, volume 120 of Graduate Texts in Mathematics (New York: Springer-Verlag, 1989). ISBN 978-0-387-97017-2.CrossRefGoogle Scholar