No CrossRef data available.
Article contents
Eine kritische Bemerkung zu Darstellungen der Schauderschen Beweistechnik für elliptische lineare Differentialgleichungen
Published online by Cambridge University Press: 14 November 2011
Synopsis
The object of this paper is to demonstrate, that with the open mapplng theorem of S.Banach one can prove very easily the following estimate
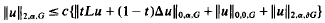
for all u ∈ C2,α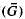 and 0 ≤ t ≤ 1, if one knows, that for all bounded G ⊂ Rn, with boundary ∂G ∈ C2,α and for all (f, g) ∈ C0,α
and 0 ≤ t ≤ 1, if one knows, that for all bounded G ⊂ Rn, with boundary ∂G ∈ C2,α and for all (f, g) ∈ C0,α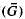 × C2,α (∂G) Dirichle's problem Δu = f, u|∂G = g has a solution u ∈ C2,α
× C2,α (∂G) Dirichle's problem Δu = f, u|∂G = g has a solution u ∈ C2,α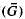 . This estimate can be used to solve Dirichle's problem for a general linear elliptic equation by Schauder's method.
. This estimate can be used to solve Dirichle's problem for a general linear elliptic equation by Schauder's method.
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 80 , Issue 3-4 , 1978 , pp. 177 - 182
- Copyright
- Copyright © Royal Society of Edinburgh 1978
References
1Barrar, R. B.On Schauder's Paper on linear elliptic differential equations. J. Math. Anal. Appl. 3 (1961), 171–195.CrossRefGoogle Scholar
2Boboc, N. and Mustatǎ, P.Remarks on the existence of solutions of the Dirichlet problem for strongly elliptic linear operators of second order. Bull. Math. Soc. Sci. Math. R. S. Roumanie. 10 (1966), 75–85.Google Scholar
3Graves, L. M. The Estimates of Schauder and their Applications to Existence Theorems for Elliptic Differential Equations. Univ. Chicago, Invest. Theory Part. Diff. Eq. Techn. Report 1 (1956).Google Scholar
4Kellogg, O. D.On the derivatives of harmonic functions on the boundary. Trans. Amer. Math. Soc. 33 (1931), 486–510.CrossRefGoogle Scholar
5König, M.Über des Verhalten der Lösung des Dirichlet-problems am Rand des Gebietes, wenn der Rand zur Klasse C 2,α gehört. Proc. Roy. Soc. Edinburgh Sect. A, 80 (1978), 163–176.CrossRefGoogle Scholar
6Ladyzhenskaya, O. A. and Uralt'seva, N. N.Linear and Quasilinear Elliptic Equations (London: Academic Press, 1968).Google Scholar
7Schauder, J.Über lineare elliptische Differential-gleichunger zweiter Ordnung. Math. Z. 38 (1934), 257–282.CrossRefGoogle Scholar


