Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-28T02:33:20.841Z Has data issue: false hasContentIssue false
  • English
  • Français

Effects of a sharp pressure rise on a compressible laminar boundary layer, when the Prandtl number is σ = 0.72*

Published online by Cambridge University Press:  14 November 2011

N. Curle
N. Curle
Affiliation:
Department of Applied Mathematics, University of St Andrews
Get access Rights & Permissions [Opens in a new window]

Synopsis

Following an earlier paper (Curle 1978) we consider a compressible laminar boundary layer with uniform pressure when the distance x along the wall satisfies x < x0 and a prescribed large adverse pressure gradient when x > x0. The viscosity and absolute temperature are again taken to be proportional, but the Prandtl number is no longer assumed to be unity. After applying the Illingworth-Stewartson transformation, the transformed external velocity u1(x) is chosen so that

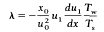
is large and constant, where Ts is the stagnation temperature, Tw is the (constant) Wall temperature and u0 is the upstream value of u1(x).

The flow reacts to this sharp pressure rise mainly in a thin inner sublayer, so inner and outer asymptotic expansions are derived and matched for functions F and S which determine the stream function and the temperature.

The skin friction, heat transfer, displacement thickness and momentum thickness are determined as functions of 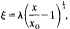, andinvolve two parameters B1, B2, which depend upon the Mach number and the walltemperature. Detailed numerical calculations are presented here for σ = 0.72. In particular, it is seen that the heat transfer rate varies roughly like σ⅓ except near to separation, where it varies like σ¼.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 84 , Issue 1-2 , 1979 , pp. 153 - 171
Copyright
Copyright © Royal Society of Edinburgh 1979

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Akinrelere, E. A.. Private communication (1977).Google Scholar
2Blasius, H.. Grenzschichten in Flüssigkeiten mit kleiner Reibung. Z. Math. Phys. 56 (1908), 1–37.Google Scholar
3Buckmaster, J.. The behaviour of a laminar compressible boundary layer on a cold wall near a point of zero skin friction. J. Fluid Mech. 44 (1970), 237–247.CrossRefGoogle Scholar
4Curle, N.. Development and separation of a laminar boundary layer, under the action of a very sharp constant adverse pressure gradient. Proc. Roy. Soc. Edinburgh Sect. A 74 (1976), 119–134.CrossRefGoogle Scholar
5Curle, N.. Development and separation of a compressible laminar boundary layer under the action of avery sharp adverse pressure gradient. J. Fluid Mech. 84 (1978), 385–400.CrossRefGoogle Scholar
6Curle, N. and Davies, H. J.. Modem Fluid Dynamics, Vol. II, p. 275. (New York: Van Nostrand Reinhold, 1971).Google Scholar
7Illingworth, C. R.. Steady flow in the laminar boundary layer of a gas. Proc. Roy. Soc. London Ser. A 199 (1949), 533–558.Google Scholar
8Leipmann, H. W.. A simple derivation of Lighthill's heat transfer formula. J. Fluid Mech. 3 (1958), 357–360.CrossRefGoogle Scholar
9Lighthill, M. J.. Contributions to the theory of heat transfer through a laminar boundary layer. Proc. Roy. Soc. London Ser. A 202 (1950), 359–377.Google Scholar
10Pohlhausen, E.. Der Warmeaustrausch zwischen festen Körpern und Flüssigkeiten mit kleiner Reibung and kleiner Wärmeleitung. Z. Angew. Math. Mech. 1 (1921), 115–121.CrossRefGoogle Scholar
11Stewartson, K.. Correlated incompressible and compressible boundary layers. Proc. Roy. Soc. London Ser. A 200 (1949), 84–100.Google Scholar
12Stratford, B. S.. Flow in the laminar boundary layer near separation. Aero. Res. Counc. R & M 3002 (1954).Google Scholar