No CrossRef data available.
Published online by Cambridge University Press: 25 November 2024
In this article, we consider some critical Brézis-Nirenberg problems in dimension 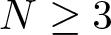 $N \geq 3$ that do not have a solution. We prove that a supercritical perturbation can lead to the existence of a positive solution. More precisely, we consider the equation:
$N \geq 3$ that do not have a solution. We prove that a supercritical perturbation can lead to the existence of a positive solution. More precisely, we consider the equation: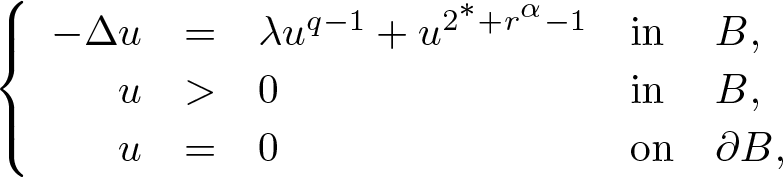 \begin{equation*}\left\{\begin{array}{rllll}-\Delta u & = & \lambda u^{q-1} + u^{2^*+ r^\alpha -1} & \mbox{in} & B, \\u & \gt & 0 & \mbox{in} & B, \\u&=&0 & \mbox{on} & \partial B,\\\end{array}\right.\end{equation*}
\begin{equation*}\left\{\begin{array}{rllll}-\Delta u & = & \lambda u^{q-1} + u^{2^*+ r^\alpha -1} & \mbox{in} & B, \\u & \gt & 0 & \mbox{in} & B, \\u&=&0 & \mbox{on} & \partial B,\\\end{array}\right.\end{equation*}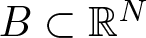 $B \subset \mathbb{R}^N$ is a unit ball centred at the origin,
$B \subset \mathbb{R}^N$ is a unit ball centred at the origin, 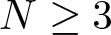 $N\geq 3$,
$N\geq 3$, 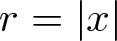 $r=\vert x \vert$,
$r=\vert x \vert$, 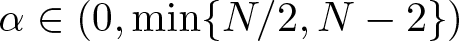 $\alpha \in (0,\min\{N/2,N-2\})$, λ is a fixed real parameter and
$\alpha \in (0,\min\{N/2,N-2\})$, λ is a fixed real parameter and 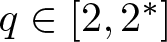 $q\in [2,2^*]$. This class of problems can be interpreted as a perturbation of the classical Brézis–Nirenberg problem by the term rα at the exponent, making the problem supercritical when
$q\in [2,2^*]$. This class of problems can be interpreted as a perturbation of the classical Brézis–Nirenberg problem by the term rα at the exponent, making the problem supercritical when 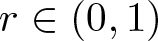 $r \in (0,1)$. More specifically, we study the effect of this supercritical perturbation on the existence of solutions. In particular, when N = 3, an interesting and unexpected phenomenon occurs. We obtain the existence of solutions for λ in a range where the Brézis–Nirenberg problem has no solution.
$r \in (0,1)$. More specifically, we study the effect of this supercritical perturbation on the existence of solutions. In particular, when N = 3, an interesting and unexpected phenomenon occurs. We obtain the existence of solutions for λ in a range where the Brézis–Nirenberg problem has no solution.