Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-06T11:48:13.979Z Has data issue: false hasContentIssue false
  • English
  • Français

Dn-forced symmetry breaking of O(2)-equivariant problems

Published online by Cambridge University Press:  12 July 2007

Jacques-Elie Furter  and
Angela Maria Sitta
Jacques-Elie Furter
Affiliation:
Department of Mathematical Sciences, Brunel University, Uxbridge UB8 3PH, UK ([email protected])
Angela Maria Sitta
Affiliation:
Departamento de Matemática, IBILCE-UNESP, Rua Cristovâo Colombo 2265, São José do Rio Preto, Brazil ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We use singularity theory to classify forced symmetry-breaking bifurcation problems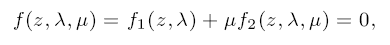 where f1 is O(2)-equivariant and f2 is Dn-equivariant with the orthogonal group actions on z ∈ R2. Forced symmetry breaking occurs when the symmetry of the equation changes when parameters are varied. We explicitly apply our results to the branching of subharmonic solutions in a model periodic perturbation of an autonomous equation and sketch further applications.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 132 , Issue 5 , October 2002 , pp. 1185 - 1218
Copyright
Copyright © Royal Society of Edinburgh 2002

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)