Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Herrero, Domingo A.
1988.
Special Classes of Linear Operators and Other Topics.
p.
125.
Marcoux, Laurent
1991.
On the distance between unitary orbits of weighted shifts.
Transactions of the American Mathematical Society,
Vol. 326,
Issue. 2,
p.
585.
Zhu, Sen
and
Ji, YouQing
2011.
Similarity orbits in the Calkin algebra.
Science China Mathematics,
Vol. 54,
Issue. 6,
p.
1225.
Skoufranis, Paul
2013.
Closed unitary and similarity orbits of normal operators in purely infiniteC⁎-algebras.
Journal of Functional Analysis,
Vol. 265,
Issue. 3,
p.
474.
Hu, Shanwen
and
Lin, Huaxin
2015.
Distance between unitary orbits of normal elements in simpleC⁎-algebras of real rank zero.
Journal of Functional Analysis,
Vol. 269,
Issue. 2,
p.
355.
Skoufranis, Paul
2016.
Closed convex hulls of unitary orbits in C⁎-algebras of real rank zero.
Journal of Functional Analysis,
Vol. 270,
Issue. 4,
p.
1319.


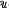 (s) denote the unitary orbit of
(s) denote the unitary orbit of