Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-05T19:54:30.976Z Has data issue: false hasContentIssue false
  • English
  • Français

Differential Operators of infinite order

Published online by Cambridge University Press:  14 November 2011

Einar Hille
Einar Hille
Affiliation:
La Jolla, California, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Synopsis

The differential operators in question are of the form G(DZ) where G(w)is an entire function of order at most 1/n and minimal type while Dz is a linear differential operator of order n with coefficients which are entire ( = integral) functions of z, usually polynomials. This class of operators form a natural generalization of the class G(d/dz) studied during the first half of the century Muggli, Polya, Ritt and others. The class G(DZ) was introduced by the present author and his pupils in the 1940s. In fact, the present paper is partly based on a MS from that period, mostly devoted to the special case

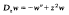
but also containing generalizations, some of which were later worked out by Klimczak. A basic tool in this paper is the characteristic series

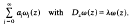
Examples are given showing that the domain of absolute convergence of such a series need neither be convex nor of finite connectivity, a question which has puzzled the author for forty odd years. Characteristic series arising from regular or singular boundary value problems for the operator Dz are used to study the inversion problem

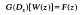
for given F(z). In particular it is shown that exp (Dx)[W(z)] = 0 has the unique solution W(z) ≡ 0. Some singular boundary value problems are considered briefly.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 86 , Issue 1-2 , 1980 , pp. 85 - 101
Copyright
Copyright © Royal Society of Edinburgh 1980

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Halm, J.. On a group of linear differential equations of the 2nd order, including Professor Chrystal's Seiche-equations. Trans. Roy. Soc. Edinburgh 41 (1905), 652–676.Google Scholar
2Hille, Einar. Note on Dirichlet's series with complex exponents. Ann. Math. 25 (1924), 261–275.Google Scholar
2AHille, Einar. Contributions to the theory of Hermitian series. Duke Math. J. 5 (1939), 895–936.Google Scholar
3Hille, Einar. A class of differential operators of infinite order. Duke Math. J. 7 (1940), 458–495.CrossRefGoogle Scholar
4Hille, Einar. On a class of orthonormal functions. Rend. Sem. Mat. Univ. Padova 25 (1956), 214–249.Google Scholar
5Hille, Einar. Über eine Klasse Differentialoperatoren von vierter Ordnung. Sitzungsber. Berlin Math. Ges. (Jahrgang 1954/1955 u. 1955/1956), 39–54.Google Scholar
6Hille, Einar. Analytic Function Theory, vol. 2 (Boston: Ginn, 1962; New York: Chelsea, 1973).Google Scholar
7Hille, Einar. Ordinary Differential Equations in the Complex Plane (New York: Wiley, 1976).Google Scholar
8Hille, Einar. On a special Weyl-Titchmarsh problem. Integral Equations and Operator Theory 1 (1978), 215–225.Google Scholar
9Klimczak, Walter J.. Differential operators of infinite order. Duke Math. J. 20 (1953), 295–319.Google Scholar
10Klimczak, Walter J.. The convergence of series of characteristic functions of the differential operator −d2/dz2 + zN, in preparation.Google Scholar
11Muggii, Hermann. Differentialgleichungen unendlich höher Ordnung mit konstanten Koeffizienten. Comment. Math. Heb. 11 (1938), 151–159.Google Scholar
12Myller, A.. Gewöhnliche Differentialgleichungen höherer Ordnung in ihrer Beziehung zu den Integralgleichungen (Göttingen Univ. Dissertation, 1906).Google Scholar
13Peabody, Mary K.. Differential operators of infinite order (Yale Univ. Doctoral Dissertation, 1944, unpublished).Google Scholar
14Polya, Georg. Untersuchungen über Lücken und Singularitäten von Potenzreihen. Math. Z. 29 (1929), 549–640.Google Scholar
15Ritt, J. F.. On a general class of linear homogeneous differenital equations of infinite order with constant coefficients. Trans. Amer. Math. Soc. 18 (1917), 27–49.CrossRefGoogle Scholar
16Titchmarsh, E. C.. Eigenfunction expansions associated with second-order differential equations (Oxford: Clarendon, 1948).Google Scholar