Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-23T16:03:21.906Z Has data issue: false hasContentIssue false
  • English
  • Français

Convergence of equilibria for bending-torsion models of rods with inhomogeneities

Part of: Equilibrium (steady-state) problems Elastic materials Homogenization, determination of effective properties Material properties given special treatment Thin bodies, structures

Published online by Cambridge University Press:  24 January 2019

Matthäus Pawelczyk
Matthäus Pawelczyk*
Affiliation:
FB Mathematik, TU Dresden, 0 1062 Dresden, Germany ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove that, in the limit of vanishing thickness, equilibrium configurations of inhomogeneous, three-dimensional non-linearly elastic rods converge to equilibrium configurations of the variational limit theory. More precisely, we show that, as 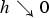$h\searrow 0$, stationary points of the energy 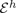, for a rod 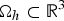$\Omega _h\subset {\open R}^3$ with cross-sectional diameter h, subconverge to stationary points of the Γ-limit of 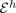, provided that the bending energy of the sequence scales appropriately. This generalizes earlier results for homogeneous materials to the case of materials with (not necessarily periodic) inhomogeneities.

Keywords

elasticitydimension reductionhomogenizationconvergence of equilibria

MSC classification

Primary: 74K10: Rods (beams, columns, shafts, arches, rings, etc.)
Secondary: 74B20: Nonlinear elasticity 74G10: Analytic approximation of solutions (perturbation methods, asymptotic methods, series, etc.) 74E30: Composite and mixture properties 74Q05: Homogenization in equilibrium problems
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 150 , Issue 1 , February 2020 , pp. 233 - 260
Copyright
Copyright © Royal Society of Edinburgh 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Ball, J. M.. Minimizers and the Euler-Lagrange equations. In Trends and applications of pure mathematics to mechanics (Palaiseau, 1983), volume 195 of Lecture Notes in Phys., pp. 1–4 (Berlin: Springer, 1984).Google Scholar
2Ball, J. M.. Some open problems in elasticity. In Geometry, mechanics, and dynamics pp. 3–59 (New York: Springer, 2002).CrossRefGoogle Scholar
3Bernoulli, J.. Quadratura curvae, e cujus evolutione describitur inflexae laminae curvatura. In Die Werke von Jakob Bernoulli pp. 223–227 (Birkhäuser, 1692). Med. CLXX; Ref. UB: L Ia 3, pp. 211–212.Google Scholar
4Braides, A., Fonseca, I. and Francfort, G.. 3D-2D asymptotic analysis for inhomogeneous thin films. Indiana Univ. Math. J. 49 (2000), 1367–1404.CrossRefGoogle Scholar
5Bukal, M., Pawelczyk, M., Velčić, I.. Derivation of homogenized Euler–Lagrange equations for von Kármán rods. J. Diff. Equ. 262 (2017), 5565–5605.CrossRefGoogle Scholar
6Davoli, E. and Mora, M. G.. Convergence of equilibria of thin elastic rods under physical growth conditions for the energy density. Proc. Roy. Soc. Edinburgh Sect. A 142 (2012), 501–524.CrossRefGoogle Scholar
7Euler, L.. Methodus inveniendi lineas curvas maximi minimive proprietate gaudentes, sive solutio problematis isoperimetrici lattissimo sensu accepti, chapter Additamentum 1. eulerarchive.org E065, 1744.Google Scholar
8Friesecke, G., James, R. D. and Müller, S.. A theorem on geometric rigidity and the derivation of nonlinear plate theory from three-dimensional elasticity. Comm. Pure Appl. Math. 55 (2002), 1461–1506.CrossRefGoogle Scholar
9Friesecke, G., James, R. D. and Müller, S.. A hierarchy of plate models derived from nonlinear elasticity by gamma-convergence. Arch. Ration. Mech. Anal. 180 (2006), 183–236.CrossRefGoogle Scholar
10Griso, G.. Asymptotic behavior of structures made of curved rods. Anal. Appl. (Singap.) 6 (2008a), 11–22.CrossRefGoogle Scholar
11Griso, G.. Decompositions of displacements of thin structures. J. Math. Pures Appl. (9) 89 (2008b), 199–223.CrossRefGoogle Scholar
12Le Dret, H. and Raoult, A.. The nonlinear membrane model as variational limit of nonlinear three-dimensional elasticity. J. Math. Pures Appl. (9) 74 (1995), 549–578.Google Scholar
13Levien, R.. The elastica: a mathematical history. Technical Report UCB/EECS- 2008-103, EECS Department, University of California, Berkeley, Aug 2008.Google Scholar
14Marohnić, M. and Velčić, I.. Non-periodic homogenization of bending-torsion theory for inextensible rods from 3D elasticity. Ann. Mat. Pura Appl. (4) 195 (2016), 1055–1079.CrossRefGoogle Scholar
15Mora, M.G., Müller, S.. Derivation of the nonlinear bending-torsion theory for inextensible rods by Γ-convergence. Calc. Var. Partial Diff. Equ. 18 (2003), 287–305.CrossRefGoogle Scholar
16Mora, M. G. and Müller, S.. Convergence of equilibria of three-dimensional thin elastic beams. Proc. Roy. Soc. Edinburgh Sect. A, 138 (2008), 873–896.CrossRefGoogle Scholar
17Mora, M. G., Müller, S. and Schultz, M. G.. Convergence of equilibria of planar thin elastic beams. Indiana Univ. Math. J., 56 (2007), 2413–2438.Google Scholar
18Neukamm, S.. Homogenization, linearization and dimension reduction in elasticity with variational methods. PhD thesis, Technische Universität München, 2010.Google Scholar
19Pawelczyk, M.. Convergence of equilibria for simultaneous dimension reduction and homogenization. PhD thesis, Technische Universtität Dresden, 2018. Unpublished thesis.Google Scholar
20Velčić, I.. On the general homogenization of von Kármán plate equations from three-dimensional nonlinear elasticity. Anal. Appl. (Singap.), 15 (2017), 1–49.CrossRefGoogle Scholar