In the present paper, we consider the following fractional double phase problem with nonlocal reaction: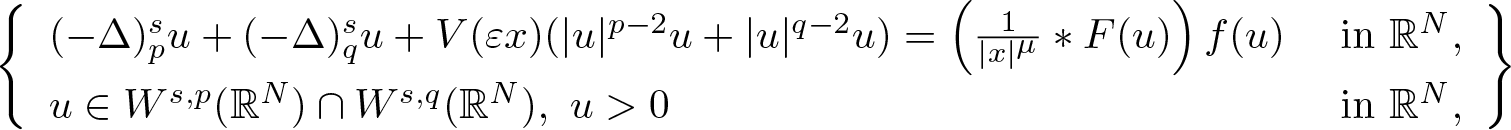

\begin{align*}\qquad \quad \left\{\begin{array}{lll}(- \Delta)_p^s u + (- \Delta)_q ^s u + V(\varepsilon x) (|u|^{p - 2} u + |u|^{q - 2} u) = \left(\frac{1}{|x|^\mu} * F(u)\right) f(u) & \ \text{in}\ \mathbb{R}^N, \\u \in W^{s,p}(\mathbb{R}^N) \cap W^{s,q}(\mathbb{R}^N) ,\ u \gt 0 & \ \text{in}\ \mathbb{R}^N,\end{array}\right\}\end{align*}

where ɛ is apositive parameter, 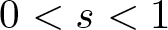$0 \lt s \lt 1$, 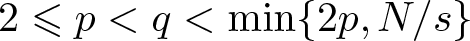$2 \leqslant p \lt q \lt \min\{2p, N / s\}$, 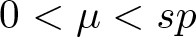$0 \lt \mu \lt sp$, 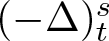$(- \Delta)_t^s$ 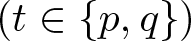$(t \in \left\{p,q\right\})$ is the fractional t-Laplace operator, the reaction term 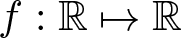$f : \mathbb{R} \mapsto \mathbb{R}$ is continuous, and the potential 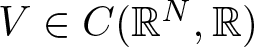$V \in C (\mathbb{R}^N , \mathbb{R})$ satisfying a local condition. Using a variational approach and topological tools (the non-standard C1-Nehari manifold analysis and the abstract category theory), multiplicity of positive solutions and concentration properties for the above problem are established. Our results extend and complement some previous contributions related to double phase variational integrals.