Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-12-01T02:17:03.241Z Has data issue: false hasContentIssue false
  • English
  • Français

Complete representation of some functionals showing the Lavrentieff phenomenon

Published online by Cambridge University Press:  12 July 2007

A. Corbo Esposito  and
T. Durante
A. Corbo Esposito
Affiliation:
Università di Cassino, Dipartimento di Automazione, Elettromagnetismo, Ingegneria dell'Informazione e Matematica Industriale, via G. Di Biasio no. 43, 03043 Cassino (FR), Italy ([email protected])
T. Durante
Affiliation:
Università di Cassino, Dipartimento di Automazione, Elettromagnetismo, Ingegneria dell'Informazione e Matematica Industriale, via G. Di Biasio no. 43, 03043 Cassino (FR), Italy ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

The functional F(u) = ∫Bf(x, Du) is considered, where B is the unit ball in R2, u varies in the set of the locally Lipschitz functions on R2 and f belongs to a family containing, as model case, the following integrand:

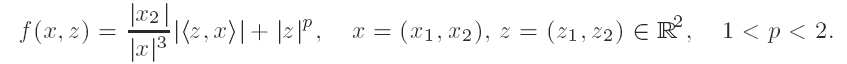
The computation of the relaxed functional F̄ is provided yielding an explicit representation formula.

This formula nevertheless is not integral, because F̄ is not a measure and does not coincide with the obvious extension of F over all W1,p(B).

This phenomenon is essentially due to the non-standard growth behaviour of f(x, z) in the variable z.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 131 , Issue 4 , August 2001 , pp. 811 - 832
Copyright
Copyright © Royal Society of Edinburgh 2001

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)