Hostname: page-component-745bb68f8f-b6zl4 Total loading time: 0 Render date: 2025-01-11T14:53:40.730Z Has data issue: false hasContentIssue false
  • English
  • Français

Coisotropic Ekeland–Hofer capacities

Part of: Differential topology Symplectic geometry, contact geometry Global differential geometry Hamiltonian and Lagrangian mechanics

Published online by Cambridge University Press:  05 September 2022

Rongrong Jin  and
Guangcun Lu
Rongrong Jin
Affiliation:
Department of Mathematics, Civil Aviation University of China, Tianjin 300300, The People's Republic of China ([email protected])
Guangcun Lu*
Affiliation:
Laboratory of Mathematics and Complex Systems, Ministry of Education, School of Mathematical Sciences, Beijing Normal University, Beijing 100875, The People's Republic of China ([email protected])
*
*Corresponding author
Get access Rights & Permissions [Opens in a new window]

Abstract

For subsets in the standard symplectic space $(\mathbb {R}^{2n},\omega _0)$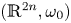 whose closures are intersecting with coisotropic subspace $\mathbb {R}^{n,k}$ 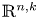we construct relative versions of the Ekeland–Hofer capacities of the subsets with respect to $\mathbb {R}^{n,k}$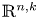, establish representation formulas for such capacities of bounded convex domains intersecting with $\mathbb {R}^{n,k}$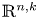. We also prove a product formula and a fact that the value of this capacity on a hypersurface $\mathcal {S}$ 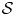of restricted contact type containing the origin is equal to the action of a generalized leafwise chord on $\mathcal {S}$.

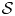Keywords

Symplectic invariantEkeland–Hofer capacitiescoisotropic

MSC classification

Primary: 53D35: Global theory of symplectic and contact manifolds 53C23: Global geometric and topological methods (à la Gromov); differential geometric analysis on metric spaces
Secondary: 70H05: Hamilton's equations 57R17: Symplectic and contact topology
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 153 , Issue 5 , October 2023 , pp. 1564 - 1608
Check for updates
Copyright
Copyright © The Author(s), 2022. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abbas, C.. A note on V. I. Arnold's chord conjecture. Int. Math. Res. Note 1999 (1999), 217–222.CrossRefGoogle Scholar
Abbas, C.. The chord problem and a new method of filling by pseudoholomorphic curves. Int. Math. Res. Note 2004 (2004), 913–927.CrossRefGoogle Scholar
Albers, P. and Frauenfelder, U.. Leaf-wise intersections and Rabinowitz Floer homology. J. Topol. Anal. 2 (2010), 77–98.CrossRefGoogle Scholar
Albers, P. and Momin, A.. Cup-length estimates for leaf-wise intersections. Math. Proc. Cambridge Philos. Soc. 149 (2010), 539–551.CrossRefGoogle Scholar
Arnol'd, V. I.. First steps in symplectic topology. Russ. Math. Surveys 41 (1986), 1–21.CrossRefGoogle Scholar
Barraud, J.-F. and Cornea, O.. Homotopic dynamics in symplectic topology. In Morse theoretic methods in nonlinear analysis and in symplectic topology (ed. P. Biran, O. Cornea and F. Lalonde). NATO Sci. Ser. II Math. Phys. Chem., vol. 217, pp. 109–148 (Dordrecht: Springer, 2006). MR2276950.CrossRefGoogle Scholar
Barraud, J.-F. and Cornea, O.. Lagrangian intersections and the Serre spectral sequence. Ann. Math. (2) 166 (2007), 657–722. https://doi.org/10.4007/annals.2007.166.657. MR 2373371.CrossRefGoogle Scholar
Biran, P. and Cornea, O.. A Lagrangian quantum homology. In New perspectives and challenges in symplectic field theory, CRM Proc. Lecture Notes, vol. 49, pp. 1–44 (Providence, RI: Am. Math. Soc., 2009). MR 2555932.CrossRefGoogle Scholar
Biran, P. and Cornea, O.. Rigidity and uniruling for Lagrangian submanifolds. Geom. Topol. 13 (2009), 2881–2989. MR 2546618.CrossRefGoogle Scholar
Cieliebak, K.. Handle attaching in symplectic homology and the chord conjecture. J. Eur. Math. Soc. 4 (2002), 115–142.CrossRefGoogle Scholar
Cristofaro-Gardiner, D. and Hutchings, M.. From one Reeb orbit to two. J. Differ. Geom. 102 (2016), 25–36.CrossRefGoogle Scholar
Dragnev, D. L.. Symplectic rigidity, symplectic fixed points, and global perturbations of Hamiltonian systems. Commun. Pure Appl. Math. 61 (2008), 346–370.CrossRefGoogle Scholar
Ekeland, I. and Hofer, H.. Symplectic topology and Hamiltonian dynamics. Math. Z. 200 (1989), 355–378.CrossRefGoogle Scholar
Ekeland, I. and Hofer, H.. Symplectic topology and Hamiltonian dynamics II. Math. Z. 203 (1990), 553–567.CrossRefGoogle Scholar
Ekholm, T., Eliashberg, Y., Murphy, E. and Smith, I.. Constructing exact Lagrangian immersions with few double points. Geom. Funct. Anal. 23 (2013), 1772–1803.CrossRefGoogle Scholar
Ginzburg, V. L.. Coisotropic intersections. Duke Math. J. 140 (2007), 111–163.CrossRefGoogle Scholar
Gromov, M.. Pseudo holomorphic curves on almost complex manifolds. Invent. Math. 82 (1985), 307–347.CrossRefGoogle Scholar
Gürel, B. Z.. Leafwise coisotropic intersections. Int. Math. Res. Note IMRN 5 (2010), 914–931.CrossRefGoogle Scholar
Hofer, H.. On the topological properties of symplectic maps. Proc. Roy. Soc. Edinburgh Sect. A 115 (1990), 25–38.CrossRefGoogle Scholar
Hofer, H. and Zehnder, E.. Symplectic invariants and Hamiltonian dynamics. Birkhäuser Advanced Texts: Basler Lehrbücher (Basel: Birkhäuser Verlag, 1994).CrossRefGoogle Scholar
Humiliére, V., Leclercq, R. and Seyfaddini, S.. Coisotropic rigidity and $C^{0}$-symplectic geometry. Duke Math. J. 164 (2015), 767–799.10.1215/00127094-2881701CrossRefGoogle Scholar
Hutchings, M. and Taubes, C. H.. Proof of the Arnold chord conjecture in three dimensions I. Math. Res. Lett. 18 (2011), 295–313.10.4310/MRL.2011.v18.n2.a8CrossRefGoogle Scholar
Hutchings, M. and Taubes, C. H.. Proof of the Arnold chord conjecture in three dimensions, II. Geom. Topol. 17 (2013), 2601–2688.CrossRefGoogle Scholar
Jin, R. and Lu, G.. Generalizations of Ekeland–Hofer and Hofer–Zehnder symplectic capacities and applications. Preprint (2019), arXiv:1903.01116v2[math.SG].Google Scholar
Jin, R. and Lu, G.. Representation formula for symmetric symplectic capacity and applications. Discrete Cont. Dyn. Sys. A 40 (2020), 4705–4765.CrossRefGoogle Scholar
Jin, R. and Lu, G.. Representation formula for coisotropic Hofer–Zehnder capacity of convex bodies and related results. Preprint (2020), arXiv:1909.08967v2[math.SG].Google Scholar
Kang, J.. Generalized Rabinowitz Floer homology and coisotropic intersections. Int. Math. Res. Note IMRN 10 (2013), 2271–2322.10.1093/imrn/rns113CrossRefGoogle Scholar
Krantz, S. G.. Convex analysis. Textbooks in Mathematics (Boca Raton, FL: CRC Press, 2015).Google Scholar
Lisi, S. and Rieser, A.. Coisotropic Hofer–Zehnder capacities and non-squeezing for relative embeddings. J. Symplectic Geom. 18 (2020), 819–865.10.4310/JSG.2020.v18.n3.a8CrossRefGoogle Scholar
Merry, W. J.. Lagrangian Rabinowitz Floer homology and twisted cotangent bundles. Geom. Dedicata 171 (2014), 345–386.10.1007/s10711-013-9903-9CrossRefGoogle Scholar
Mohnke, K.. Holomorphic disks and the chord conjecture. Ann. Math. (2) 154 (2001), 219–222.CrossRefGoogle Scholar
Moser, J.. A fixed point theorem in symplectic geometry. Acta Math. 141 (1978), 17–34.CrossRefGoogle Scholar
Rizell, G. D.. Exact Lagrangian caps and non-uniruled Lagrangian submanifolds. Ark. Mat. 53 (2015), 37–64.CrossRefGoogle Scholar
Rizell, G. D. and Sullivan, M. G.. An energy-capacity inequality for Legendrian submanifolds. J. Topol. Anal. 12 (2020), 547–623.10.1142/S1793525319500572CrossRefGoogle Scholar
Sandon, S.. On iterated translated points for contactomorphisms of $\mathbb {R}^{2}n+1$ and $\mathbb {R}^{2}n\times S^{1}$. Int. J. Math. 23 (2012), 1250042, 14 pp.CrossRefGoogle Scholar
Schlenk, F.. Embedding problems in symplectic geometry. De Gruyter Expositions in Mathematics, vol. 40 (Berlin: Walter de Gruyter GmbH & Co. KG, 2005).CrossRefGoogle Scholar
Sikorav, J.-C.. Systémes Hamiltoniens et topologie symplectique. Dipartimento di atematica dell'Universitá di Pisa, 1990. ETS, EDITRICE PISA.Google Scholar
Usher, M.. Boundary depth in Floer theory and its applications to Hamiltonian dynamics and coisotropic submanifolds. Israel J. Math. 184 (2011), 1–57.CrossRefGoogle Scholar
Ziltener, F.. Coisotropic submanifolds, leaf-wise fixed points, and presymplectic embeddings. J. Symplectic Geom. 8 (2010), 95–118.CrossRefGoogle Scholar
Ziltener, F.. On the strict Arnold chord property and coisotropic submanifolds of complex projective space. Int. Math. Res. Note IMRN 2016 (2016), 795–826.CrossRefGoogle Scholar