We consider the following Fife–Greenlee problem:

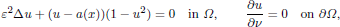
where Ω is a smooth and bounded domain in ℝn, ν is the outer unit normal to ∂Ω and a is a smooth function satisfying a(x) ∈ (–1, 1) in 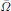. Let K, Ω– and Ω+ be the zero-level sets of a, {a < 0} and {a < 0}, respectively. We assume ∇a ≠ 0 on K. Fife and Greenlee constructed stable layer solutions, while del Pino et al. proved the existence of one unstable layer solution provided that some gap condition is satisfied. In this paper, for each odd integer m ≥ 3, we prove the existence of a sequence ε = εj → 0, and a solution 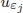with m-transition layers near K. The distance of any two layers is O(ε log(1/ε)). Furthermore, 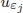converges uniformly to ±1 on the compact sets of Ω± as j → +∞