Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Müller, S.
and
Sychev, M.A.
2001.
Optimal Existence Theorems for Nonhomogeneous Differential Inclusions.
Journal of Functional Analysis,
Vol. 181,
Issue. 2,
p.
447.
Fonseca, Irene
Fusco, Nicola
and
Marcellini, Paolo
2002.
An existence result for a nonconvex variational problem via regularity.
ESAIM: Control, Optimisation and Calculus of Variations,
Vol. 7,
Issue. ,
p.
69.
Sychev, M.A.
2005.
Sets of lower semicontinuity and stability of integral functionals.
Journal de Mathématiques Pures et Appliquées,
Vol. 84,
Issue. 8,
p.
985.
Goncharov, Vladimir V.
and
Ornelas, António
2006.
On minima of a functional of the gradient: Upper and lower solutions.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 64,
Issue. 7,
p.
1437.
Celada, Pietro
Cupini, Giovanni
and
Guidorzi, Marcello
2007.
Existence and regularity of minimizers of nonconvex integrals withp-qgrowth.
ESAIM: Control, Optimisation and Calculus of Variations,
Vol. 13,
Issue. 2,
p.
343.
Mederos, Boris
Mollineda, Ramón A.
and
Camarena, Julián Antolín
2016.
Reconstruction of noisy signals by minimization of non-convex functionals.
Nonlinear Analysis: Real World Applications,
Vol. 32,
Issue. ,
p.
355.
Lussardi, Luca
and
Mascolo, Elvira
2017.
A uniqueness result for a class of non-strictly convex variational problems.
Journal of Mathematical Analysis and Applications,
Vol. 446,
Issue. 2,
p.
1687.
Sychev, Mikhail A.
Treu, Giulia
and
Colombo, Giovanni
2020.
Stable minimizers of functionals of the gradient.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 150,
Issue. 5,
p.
2642.

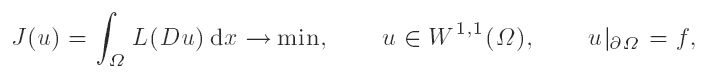 with f(·) = 〈F,·〉.
with f(·) = 〈F,·〉.