Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-24T13:45:25.358Z Has data issue: false hasContentIssue false
  • English
  • Français

Borderline gradient estimates at the boundary in Carnot groups

Part of: Partial differential equations Miscellaneous topics - Partial differential equations Elliptic equations and systems

Published online by Cambridge University Press:  02 December 2020

Ramesh Manna  and
Ram Baran Verma
Ramesh Manna
Affiliation:
TIFR Centre for Applicable Mathematics, Sharada Nagar, Chikkabommasandra, Bangalore560065, India ([email protected]; [email protected])
Ram Baran Verma
Affiliation:
SRM University Amaravati, Andhra Pradesh522502, India ([email protected]; [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

In this article, we prove the continuity of the horizontal gradient near a C1,Dini non-characteristic portion of the boundary for solutions to 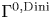$\Gamma ^{0,{\rm Dini}}$ perturbations of horizontal Laplaceans as in (1.1) below, where the scalar term is in scaling critical Lorentz space L(Q, 1) with Q being the homogeneous dimension of the group. This result can be thought of both as a sharpening of the 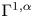$\Gamma ^{1,\alpha }$ boundary regularity result in [4] as well as a subelliptic analogue of the main result in [1] restricted to linear equations.

Keywords

Second-order subelliptic equationsborderline gradient continuityDini-domainsCarnot group

MSC classification

Primary: 35R03: Partial differential equations on Heisenberg groups, Lie groups, Carnot groups, etc. 35B65: Smoothness and regularity of solutions
Secondary: 35J25: Boundary value problems for second-order elliptic equations
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 151 , Issue 6 , December 2021 , pp. 1920 - 1953
Check for updates
Copyright
Copyright © The Author(s), 2020. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adimurthi, K. and Banerjee, A.. Borderline regularity for fully nonlinear equations in Dini domains, arXiv:1806.07652.Google Scholar
Baernstein, A.. Symmetrization in analysis (Cambridge: Cambridge University Press, 2019).CrossRefGoogle Scholar
Baldi, A., Citti, G. and Cupini, G.. Schauder estimates at the boundary for sub-Laplacians in Carnot groups, arXiv:1610.03270.Google Scholar
Banerjee, A., Garofalo, N. and Munive, I. H. Compactness methods for Γ1, α boundary Schauder estimates in Carnot groups. Calc. Var. 58 (2019), 97. (doi.org/10.1007/s00526-019-1531-2).CrossRefGoogle Scholar
Banerjee, A. and Munive, I. H.. Gradient continuity estimates for the normalized p-Poisson equation, Communications in Contemporary Mathematics, https://doi.org/10.1142/S021919971950069X.CrossRefGoogle Scholar
Bellaïche, A.. The tangent space in sub-Riemannian geometry. In Sub-Riemannian geometry (ed. A. Bellaïche and J.J.Risler). Progr. Math., vol. 144, pp. 1–78 (Basel: Birkhuser, 1996).CrossRefGoogle Scholar
Bellaïche, A. and Risler, J.. Sub-Riemannian geometry. In Progress in Mathematics, vol. 144 (Birkhäuser, Basel, 1996, viii+393 pp.)Google Scholar
Bonfiglioli, A., Lanconelli, E. and Uguzzoni, F.. Stratified Lie groups and potential theory for their sub-Laplacians (Berlin: Springer, 2007 xxvi+800 pp).Google Scholar
Caffarelli, L.. Interior a priori estimates for solutions of fully nonlinear equations. Ann. Math. 130 (1989), 189–213.CrossRefGoogle Scholar
Capogna, L. and Garofalo, N.. Boundary behavior of nonnegative solutions of subelliptic equations in NTA domains for Carnot-Caratheodory metrics. J. Fourier. Anal. Appl. 4 (1998), 403–432.CrossRefGoogle Scholar
Capogna, L. and Han, Q.. Pointwise Schauder estimates for second order linear equations in Carnot groups. In Harmonic analysis at Mount Holyoke (ed. W. Beckner, A. Nagel, A. Seeger and H. F. Smith), pp. 45–69 (South Hadley, MA, MA. 2001, Contemp. Math. 320, Amer. Math. Soc., Providence, RI, 2003).Google Scholar
Citti, G.. C ∞ regularity of solutions of a quasilinear equation related to the Levi operator. Ann. Scuola Norm. Sup. Pisa Cl. Sci. 23 (1996), 483–529.Google Scholar
Corwin, L. and Greenleaf, F. P.. Representations of nilpotent Lie groups and their applications, Part I: basic theory and examples, Cambridge studies in advanced mathematics 18 (Cambridge: Cambridge University Press, 1990).Google Scholar
Danielli, D.. Regularity at the boundary for solutions of nonlinear subelliptic equations. Indiana Univ. Math. J. 144 (1995), 269–286.Google Scholar
Danielli, D., Garofalo, N. and Petrosyan, A.. The sub-elliptic obstacle problem: C 1, α regularity of the free boundary in Carnot groups of step two. Adv. Math. 211 (2007), 485–516.CrossRefGoogle Scholar
Daskalopoulos, P., Kuusi, T. and Mingione, G.. Borderline estimates for fully nonlinear elliptic equations. Comm. Partial Differential Equations, 39 (2014), 574–590.CrossRefGoogle Scholar
David, C.. A few notes on Lorentz spaces, arXiv:1802.00244.Google Scholar
Duzaar, F. and Mingione, G.. Gradient estimates via non-linear potentials. Amer. J. Math. 123 (2011), 1093–1149.CrossRefGoogle Scholar
Folland, G. B.. Subelliptic estimates and function spaces on nilpotent Lie groups. Ark. Math. 13 (1975), 161–207.CrossRefGoogle Scholar
Folland, G. B. and Stein, E. M.. Hardy spaces on homogeneous Carnot groups. Mathematical notes, vol. 28 (Princeton, NJ: Princeton University Press, 1982, xii+285 pp).Google Scholar
Garofalo, N.. Hypoelliptic operators and some aspects of analysis and geometry of sub-Riemannian spaces. In Geometry, analysis and dynamics on sub-Riemannian manifolds (ed. Barilari, D., Boscain, U. and Sigalotti, M.), vol. 1, pp. 123–257 (Zürich: EMS Eer. Lect. Math., Eur. math. soc., 2016).Google Scholar
Gutierrez, C. and Lanconelli, E.. Schauder estimates for sub-elliptic equations. J. Evol. Equ. 9 (2009), 707–726.CrossRefGoogle Scholar
Hörmander, H.. Hypoelliptic second-order differential equations. Acta Math. 119 (1967), 147–171.CrossRefGoogle Scholar
Jerison, D. S.. The Dirichlet problem for the Kohn Laplacian on the Heisenberg group I. J. Funct. Anal. 43 (1981), 97–142.CrossRefGoogle Scholar
Jerison, D. S.. The Dirichlet problem for the Kohn Laplacian on the Heisenberg group II. J. Funct. Anal. 43 (1981), 224–257.CrossRefGoogle Scholar
Kuusi, T. and Mingione, G.. Universal potential estimates. J. Funct. Anal. 262 (2012), 4205–4269.CrossRefGoogle Scholar
Kuusi, T. and Mingione, G.. Linear potentials in nonlinear potential theory. Arch. Ration. Mech. Anal. 207 (2013), 215–246.CrossRefGoogle Scholar
Kuusi, T. and Mingione, G.. Guide to nonlinear potential estimates. Bull. Math. Sci. 4 (2014), 1–82.CrossRefGoogle ScholarPubMed
Kuusi, T. and Mingione, G.. A nonlinear Stein theorem. Calc. Var. Partial Differential Equations 51 (2014), 45–86.CrossRefGoogle Scholar
Kuusi, T. and Mingione, G.. Nonlinear potential theory of elliptic systems. Nonlinear Analysis, 138 (2016), 277–299.CrossRefGoogle Scholar
Lanconelli, E. and Uguzzoni, F.. On the Poisson kernel for the Kohn Laplacian. Rend. Mat. Appl. 17 (1997), 659–677.Google Scholar
Lions, J. L. and Magenes, E.. Non-homogeneous boundary value problems and applications, vol. I. Translated from the French by P. Kenneth. Die Grundlehren der mathematischen Wissenschaften, Band 181 (New York-Heidelberg: Springer-Verlag, 1972).Google Scholar
Lorentz, G. G.. Approximation of functions, Holt, Rinehart and Winston (New York-Chicago, Ill.-Toronto, Ont., 1966, MR 0213785).Google Scholar
Manfredi, J. J. and De Serio, V. N.. Rearrangements in Carnot groups, arXiv:1805.10595.Google Scholar
Nagel, A., Stein, E. and Wainger, S.. Balls and metrics defined by vector fields. I. Basic properties. Acta Math. 155 (1985), 103–147.CrossRefGoogle Scholar
Rothschild, L. P. and Stein, E. M.. Hypoelliptic differential operators and nilpotent groups. Acta Math. 137 (1976), 247–320.CrossRefGoogle Scholar
Simon, L.. Schauder estimates by scaling. Calc. Var. Partial Differ. Equ., 5 (1997), 391–407.CrossRefGoogle Scholar
Stein, E. M.. Some problems in harmonic analysis suggested by symmetric spaces and semi-simple groups. Actes du Congrès International des Mathématiciens (Nice, 1970), Tome 1, pp. 173–189 (Paris: Gauthier-Villars, 1971).Google Scholar
Stein, E. M.. Editors note: the differentiability of functions in ${\mathbb R}^n$. Ann. of Math. 113 (1981), 383–385.Google Scholar
Varadarajan, V. S.. Lie algebras, and Lie groups their representations (New York, Berlin, Heidelberg, Tokyo: Springer-Verlag, 1974).Google Scholar
Xu, C. J.. Regularity for quasilinear second-order subelliptic equations. Comm. Pure Appl. Math. 45 (1992), 77–96.CrossRefGoogle Scholar
Xu, C. and Zuily, C.. Higher interior regularity for quasilinear subelliptic systems. Calc. Var. Partial Differ. Equ. 5 (1997), 323–343.CrossRefGoogle Scholar