Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Delgado, M.
and
Suárez, A.
2003.
Nonnegative solutions for the degenerate logistic indefinite sublinear equation.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 52,
Issue. 1,
p.
127.
Arcoya, David
and
Carmona, José
2003.
Quasilinear elliptic problems interacting with its asymptotic spectrum.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 52,
Issue. 6,
p.
1591.
Gámez, José L.
and
Ruiz-Hidalgo, Juan F.
2008.
A detailed analysis on local bifurcation from infinity for nonlinear elliptic problems.
Journal of Mathematical Analysis and Applications,
Vol. 338,
Issue. 2,
p.
1458.
Huy, Nguyen Bich
Thanh, Nguyen Duy
and
Thanh, Tran Dinh
2012.
On the structure of unbounded positive solutions to the quasilinear logistic equation.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 75,
Issue. 8,
p.
3682.
Motreanu, Dumitru
Motreanu, Viorica Venera
and
Papageorgiou, Nikolaos
2014.
Topological and Variational Methods with Applications to Nonlinear Boundary Value Problems.
p.
223.
Motreanu, Dumitru
Motreanu, Viorica Venera
and
Papageorgiou, Nikolaos
2014.
Topological and Variational Methods with Applications to Nonlinear Boundary Value Problems.
p.
271.
Motreanu, Dumitru
Motreanu, Viorica Venera
and
Papageorgiou, Nikolaos
2014.
Topological and Variational Methods with Applications to Nonlinear Boundary Value Problems.
p.
15.
Motreanu, Dumitru
Motreanu, Viorica Venera
and
Papageorgiou, Nikolaos
2014.
Topological and Variational Methods with Applications to Nonlinear Boundary Value Problems.
p.
97.
Motreanu, Dumitru
Motreanu, Viorica Venera
and
Papageorgiou, Nikolaos
2014.
Topological and Variational Methods with Applications to Nonlinear Boundary Value Problems.
p.
45.
Motreanu, Dumitru
Motreanu, Viorica Venera
and
Papageorgiou, Nikolaos
2014.
Topological and Variational Methods with Applications to Nonlinear Boundary Value Problems.
p.
1.
Motreanu, Dumitru
Motreanu, Viorica Venera
and
Papageorgiou, Nikolaos
2014.
Topological and Variational Methods with Applications to Nonlinear Boundary Value Problems.
p.
303.
Motreanu, Dumitru
Motreanu, Viorica Venera
and
Papageorgiou, Nikolaos
2014.
Topological and Variational Methods with Applications to Nonlinear Boundary Value Problems.
p.
61.
Motreanu, Dumitru
Motreanu, Viorica Venera
and
Papageorgiou, Nikolaos
2014.
Topological and Variational Methods with Applications to Nonlinear Boundary Value Problems.
p.
141.
Motreanu, Dumitru
Motreanu, Viorica Venera
and
Papageorgiou, Nikolaos
2014.
Topological and Variational Methods with Applications to Nonlinear Boundary Value Problems.
p.
201.
Motreanu, Dumitru
Motreanu, Viorica Venera
and
Papageorgiou, Nikolaos
2014.
Topological and Variational Methods with Applications to Nonlinear Boundary Value Problems.
p.
181.
Cintra, Willian
Rodrigo, Cristian Morales
and
Suárez, Antonio
2017.
Combining linear and fast diffusion in a nonlinear elliptic equation.
Calculus of Variations and Partial Differential Equations,
Vol. 56,
Issue. 1,
Ambrosetti, Antonio
and
Arcoya, David
2017.
Positive Solutions of Elliptic Kirchhoff Equations.
Advanced Nonlinear Studies,
Vol. 17,
Issue. 1,
p.
3.
Delgado, M.
Duarte, I.B.M.
and
Suárez, A.
2019.
Positive solutions of a nonlocal singular elliptic equation by means of a non-standard bifurcation theory.
Journal of Mathematical Analysis and Applications,
Vol. 469,
Issue. 2,
p.
897.
Cintra, W.
Morales-Rodrigo, C.
and
Suárez, A.
2019.
Unilateral global bifurcation for a class of quasilinear elliptic systems and applications.
Journal of Differential Equations,
Vol. 267,
Issue. 1,
p.
619.
Figueiredo-Sousa, Tarcyana S.
Morales-Rodrigo, Cristian
and
Suárez, Antonio
2020.
Some superlinear problems with nonlocal diffusion coefficient.
Journal of Mathematical Analysis and Applications,
Vol. 482,
Issue. 1,
p.
123519.
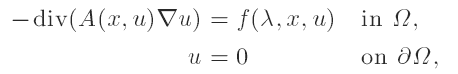 ,
where Ω is a bounded open domain in RN with smooth boundary. Under suitable assumptions on the matrix A(x, s), and depending on the behaviour of the function f near u = 0 and near u = +∞, we can use bifurcation theory in order to give a quite complete analysis on the set of positive solutions. We will generalize in different directions some of the results in the papers by Ambrosetti et al., Ambrosetti and Hess, and Artola and Boccardo.
,
where Ω is a bounded open domain in RN with smooth boundary. Under suitable assumptions on the matrix A(x, s), and depending on the behaviour of the function f near u = 0 and near u = +∞, we can use bifurcation theory in order to give a quite complete analysis on the set of positive solutions. We will generalize in different directions some of the results in the papers by Ambrosetti et al., Ambrosetti and Hess, and Artola and Boccardo.