Hostname: page-component-745bb68f8f-s22k5 Total loading time: 0 Render date: 2025-02-10T08:28:10.013Z Has data issue: false hasContentIssue false
  • English
  • Français

Asymptotic stability of rarefaction wave for the compressible Navier‐Stokes‐Korteweg equations in the half space

Part of: Partial differential equations Magnetohydrodynamics and electrohydrodynamics

Published online by Cambridge University Press:  23 July 2021

Yeping Li ,
Jing Tang  and
Shengqi Yu
Yeping Li
Affiliation:
School of Sciences, Nantong University, Nantong 226019, P.R. China [email protected]
Jing Tang
Affiliation:
School of Sciences, Nantong University, Nantong 226019, P.R. China [email protected]
Shengqi Yu
Affiliation:
School of Sciences, Nantong University, Nantong 226019, P.R. China [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this study, we are concerned with the asymptotic stability towards a rarefaction wave of the solution to an outflow problem for the Navier-Stokes Korteweg equations of a compressible fluid in the half space. We assume that the space-asymptotic states and the boundary data satisfy some conditions so that the time-asymptotic state of this solution is a rarefaction wave. Then we show that the rarefaction wave is non-linearly stable, as time goes to infinity, provided that the strength of the wave is weak and the initial perturbation is small. The proof is mainly based on 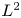$L^{2}$-energy method and some time-decay estimates in 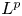$L^{p}$-norm for the smoothed rarefaction wave.

Keywords

Compressible Navier-Stokes-Korteweg equationRarefaction waveAsymptotic stabilityEnergy method

MSC classification

Primary: 76W05: Magnetohydrodynamics and electrohydrodynamics
Secondary: 35B40: Asymptotic behavior of solutions
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 152 , Issue 3 , June 2022 , pp. 756 - 779
Check for updates
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bian, D.-F., Yao, L. and Zhu, C.-J.. Vanishing capillarity limit of the compressible fluid models of Korteweg type to the Navier-Stokes equations. SIAM J. Math. Anal. 46 (2014), 1633–1650.CrossRefGoogle Scholar
Bresch, D., Desjardins, B., Lin, C.-K.. On some compressible fluid models: Korteweg lubrication and shallow water systems. Comm. Partial Differ. Equ. 28 (2003), 843–868.CrossRefGoogle Scholar
Cai, H., Tan, Z. and Xu, Q.-J.. Time periodic solutions to Navier-Stokes-Korteweg system with friction. Discrete Contin. Dyn. Syst. 36 (2016), 611–629.CrossRefGoogle Scholar
Charve, F. and Haspot, B.. Existence of global strong solution and vanishing capillarity-viscosity limit in one dimension for the Korteweg system. SIMA J. Math. Anal. 45 (2014), 469–494.CrossRefGoogle Scholar
Chen, Z.-Z.. Asymptotic stability of strong rarefaction waves for the compressible fluid models of Korteweg type. J. Math. Anal. Appl. 394 (2012), 438–448.CrossRefGoogle Scholar
Chen, Z.-Z., Chai, X.-J., Dong, B.-Q. and Zhao, H.-J.. Global classical solutions to the one-dimensional compressible fluid models of Korteweg type with large initial data. J. Diff. Eqns. 259 (2015), 4376–4411.CrossRefGoogle Scholar
Chen, Z.-Z., He, L. and Zhao, H.-J.. Nonlinear stability of traveling wave solutions for the compressible fluid models of Korteweg type. J. Math. Anal. Appl. 422 (2015), 1213–1234.CrossRefGoogle Scholar
Chen, Z.-Z. and Li, Y.-P.. Asymptotic behavior of solutions to an impermeable wall problem of the compressible fluid models of Korteweg type with density-dependent viscosity and capillarity. SIAM J. Math.Anal. 53 (2021), 1434–1473.CrossRefGoogle Scholar
Chen, Z.-Z., Li, Y.-P. and Sheng, M.-D.. Asymptotic stability of viscous shock profiles for the 1D compressible Navier-Stokes-Korteweg system with boundary effect. Dyn. Partial Differ. Equ. 16 (2019), 225–251.CrossRefGoogle Scholar
Danchin, R. and Desjardins, B.. Existence of solutions for compressible fluid models of Korteweg type. Ann. Inst. Henri Poincaré Anal. Non linéaire 18 (2001), 97–133.CrossRefGoogle Scholar
Dunn, J. E. and Serrin, J.. On the thermodynamics of interstitial working. Arch. Rational Mech. Anal. 88 (1985), 95–133.CrossRefGoogle Scholar
Fan, L., Liu, H., Wang, T. and Zhao, H.. Inflow problem for the one-dimensional compressible Navier-Stokes equations under large initial perturbation. J. Diff. Eqns. 257 (2014), 3521–3553.CrossRefGoogle Scholar
Germain, P., LeFloch, P. G.. Finite energy method for compressible fluids: the Navier-Stokes-Korteweg model. Comm. Pure Appl. Math. 69 (2016), 3–61.CrossRefGoogle Scholar
Haspot, B.. Existence of global weak solution for compressible fluid models of Korteweg type. J. Math. Fluid Mech. 13 (2011), 223–249.CrossRefGoogle Scholar
Haspot, B.. Existence of global strong solution for the compressible Navier-Stokes system and the Korteweg system in two-dimension. Methods Appl. Anal. 20 (2013), 141–164.CrossRefGoogle Scholar
Haspot, B.. Existence of global strong solution for Korteweg system with large infinite energy initial data. J. Math. Anal. Appl. 438 (2016), 395–443.CrossRefGoogle Scholar
Hattori, H. and Li, D.. Solutions for two dimensional system for materials of Korteweg type. SIAM J. Math. Anal. 25 (1994), 85–98.CrossRefGoogle Scholar
Hattori, H. and Li, D.. Golobal solutions of a high dimensional system for Korteweg materials. J. Math. Anal. Appl. 198 (1996), 84–97.CrossRefGoogle Scholar
Hong, H.. Stationary solutions to outflow problem for 1-D compressible fluid models of Korteweg type: Existence, stability and convergence rate. Nonlinear Anal. Real World Appl. 53 (2020), 103055.CrossRefGoogle Scholar
Hong, H. and Wang, T.. Stability of stationary solutions to the inflow problem for full compressible Navier-Stokes equations with a large initial perturbation. SIAM J. Math. Anal. 49 (2017), 2138–2166.CrossRefGoogle Scholar
Hou, X.-F., Peng, H.-Y. and Zhu, C.-J.. Global classical solutions to the 3D Navier-Stokes-Korteweg equations with small initial energy. Anal. Appl. 16 (2018), 55–84.CrossRefGoogle Scholar
Huang, F., Li, J. and Shi, X.. Asymptotic behavior of solutions to the full compressible Navier-Stokes equations in the half space. Comm. Math. Sci. 8 (2010), 639–654.CrossRefGoogle Scholar
Huang, F.-M. and Matsumura, A.. Stability of a composite wave of two viscous shock waves for the full compressible Navier-Stokes equations. Comm. Math. Phys. 289 (2009), 841–861.CrossRefGoogle Scholar
Huang, F.-M., Matsumura, A. and Shi, X.-D.. Viscous shock wave and boundary layer solution to an inflow problem for compressible viscous gas. Comm. Math. Phys. 239 (2003), 261–285.CrossRefGoogle Scholar
Huang, F. and Qin, X.. Stability of boundary layer and rarefaction wave to an outflow problem for compressible Navier-Stokes equations under large perturbation. J. Diff. Eqns. 246 (2009), 4077–4096.CrossRefGoogle Scholar
Kawashima, S., Nishibata, S. and Zhu, P.-C.. Asympotic stability of the stationary solution to the compressible Navier-Stokes equations in the half space. Comm. Math. Phys. 240 (2003), 483–500.CrossRefGoogle Scholar
Kawashima, S. and Zhu, P.-C.. Asymptotic stability of nonlinear wave for the compressible Navier-Stokes equations in the half space. J. Diff. Eqns. 244 (2008), 3151–3179.CrossRefGoogle Scholar
Kawashima, S. and Zhu, P.-C.. Asymptotic stability of rarefaction wave for the Navier-Stokes equations for a compressible fluid in the half space. Arch. Rati. Mech. Anal. 194 (2009), 105–132.CrossRefGoogle Scholar
Korteweg, D. J.. Sur la forme que prennent les équations des mouvement des fluids si l'on tient comple des forces capillaries par des variations de densité. Arch. Neerl. Sci. Exactes Nat. Ser. II 6 (1901), 1–24.Google Scholar
Kotschote, M.. Strong solutions for a compressible fluid model of Korteweg type. Ann. Inst. Henri Poincaré Anal. Non linéaire 25 (2008), 679–696.CrossRefGoogle Scholar
Kotschote, M.. Existence and time-asymptotics of global strong solutions to dynamic Korteweg models. Indiana Univ. Math. J. 63 (2014), 21–51.CrossRefGoogle Scholar
Li, Y.-P.. Global existence and optimal decay rate of the compressible Navier-Stokes-Korteweg equations with external force. J. Math. Anal. Appl. 388 (2012), 1218–1232.CrossRefGoogle Scholar
Li, Y.-P. and Luo, Z.. Zero-capillarity-viscosity limit to rarefaction waves for the one-dimensional compressible Navier-Stokes-Korteweg equations. Math. Meth. Appl. Sci. 39 (2016), 5513–5528.CrossRefGoogle Scholar
Li, Y.-P. and Zhu, P.-C.. Zero-viscosity-capillarity limit to rarefaction wave with vacuum for the compressible Navier-Stokes-Korteweg equations. J. Math. Phy. 61 (2020), 111501.CrossRefGoogle Scholar
Li, Y.-P. and Zhu, P.-C.. Asymptotic stability of the stationary solution to the Navier-Stokes-Korteweg equations of compressible fluids. Nonlinear Anal.: Real World Appl. 57 (2021), 103193.CrossRefGoogle Scholar
Matsumura, A.. Inflow and outflows problems in the half space for a one-dimensional isentropic model system of compressible viscous gas. Methods Appl. Anal. 8 (2001), 645–666.CrossRefGoogle Scholar
Matsumura, A. and Mei, M.. Convergence to traveling front of solutions of the $p$-system with viscosity in the presence of a boundary. Arch. Ration. Mech. Anal. 146 (1999), 1–22.CrossRefGoogle Scholar
Matsumura, A. and Nishihara, K.. Global asymptotics toward rarefaction waves for solution of the viscous $p$-system with boundary effect. Quart. Appl. Math. 58 (2000), 69–83.CrossRefGoogle Scholar
Matsumura, A. and Nishihara, K.. Large-time behavior of solutions to an inflow problem in the half space for a one-dimensional isentropic model system for compressible viscous gas. Comm. Math. Phys. 222 (2001), 449–474.CrossRefGoogle Scholar
Qin, X. and Wang, Y.. Stability of wave patterns to the inflow problem of full compressible Navier-Stokes equations. SIAM J. Math. Anal. 41 (2009), 2057–2087.CrossRefGoogle Scholar
Qin, X. and Wang, Y.. Large time behavior of solutions to the inflow problem of full compressible Navier-Stokes equations. SIAM J. Math. Anal. 43 (2011), 341–366.CrossRefGoogle Scholar
Tan, Z. and Wang, Y.. Large time behavior of solutions to the isentropic compressible fluid models of Korteweg type in $\mathbb {R}^{3}$. Comm. Math. Sci. 10 (2012), 1207–1223.CrossRefGoogle Scholar
Tan, Z., Wang, H.-Q. and Xu, J.-K.. Global existence and optimal $L^{2}$ decay rate for the strong solutions to the compressible fluid models of Korteweg type. J. Math. Anal. Appl. 390 (2012), 181–187.CrossRefGoogle Scholar
Tan, Z. and Zhang, R.-F.. Optimal decay rates of the compressible fluid models of Korteweg type. Z. Angew. Math. Phys. 65 (2014), 279–300.CrossRefGoogle Scholar
Tsyganov, E.. Global existence and asymptotic convergence of weak solutions for the one-dimensional Navier-Stokes equations with capillarity and nonmonotonic pressure. J. Differ. Equ. 245 (2008), 3936–3955.CrossRefGoogle Scholar
Van der Waals, J. D.. Thermodynamische Theorie der Kapillarität unter Voraussetzung stetiger Dichteänderung. Z. Phys. Chem. 13 (1894), 657–725.CrossRefGoogle Scholar
Wang, Y.-J. and Tan, Z.. Optimal decay rates for the compressible fluid models of Korteweg type. J. Math. Anal. Appl. 379 (2011), 256–271.CrossRefGoogle Scholar
Wang, W.-J. and Wang, W.-K.. Decay rate of the compressible Navier-Stokes-Korteweg equations with potential force. Dis. Contin. Dyn. Syst. 35 (2015), 513–536.CrossRefGoogle Scholar