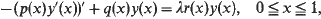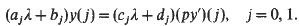Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Binding, P. A.
and
Browne, Patrick J.
1997.
Oscillation theory for indefinite Sturm-Liouville problems with eigenparameter-dependent boundary conditions.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 127,
Issue. 6,
p.
1123.
Browne, Patrick J
and
Sleeman, B D
1997.
A uniqueness theorem for inverse eigenparameter dependent Sturm - Liouville problems.
Inverse Problems,
Vol. 13,
Issue. 6,
p.
1453.
Browne, Patrick J.
1998.
A Prüfer approach to half-linear Sturm-Liouville problems.
Proceedings of the Edinburgh Mathematical Society,
Vol. 41,
Issue. 3,
p.
573.
Bhattacharyya, T
Binding, P.A
and
Seddighi, K
2001.
Multiparameter Sturm–Liouville Problems with Eigenparameter Dependent Boundary Conditions.
Journal of Mathematical Analysis and Applications,
Vol. 264,
Issue. 2,
p.
560.
Binding, Paul A.
Browne, Patrick J.
and
Watson, Bruce A.
2004.
Recovery of the m-function from spectral data for generalized Sturm–Liouville problems.
Journal of Computational and Applied Mathematics,
Vol. 171,
Issue. 1-2,
p.
73.
Guliyev, Namig J
2005.
Inverse eigenvalue problems for Sturm–Liouville equations with spectral parameter linearly contained in one of the boundary conditions.
Inverse Problems,
Vol. 21,
Issue. 4,
p.
1315.
Dehghani Tazehkand, I.
and
Jodayree Akbarfam, A.
2011.
On Inverse Sturm-Liouville Problems with Spectral Parameter Linearly Contained in the Boundary Conditions.
ISRN Mathematical Analysis,
Vol. 2011,
Issue. ,
p.
1.
Aliyev, Ziyatkhan S.
and
Kerimov, Nazim B.
2012.
Spectral Properties of the Differential Operators of the Fourth-Order with Eigenvalue Parameter Dependent Boundary Condition.
International Journal of Mathematics and Mathematical Sciences,
Vol. 2012,
Issue. ,
p.
1.
Aliev, Z. S.
and
Dun’yamalieva, A. A.
2015.
Defect basis property of a system of root functions of a Sturm–Liouville problem with spectral parameter in the boundary conditions.
Differential Equations,
Vol. 51,
Issue. 10,
p.
1249.
Gao, Chenghua
and
Ma, Ruyun
2016.
Eigenvalues of discrete Sturm–Liouville problems with eigenparameter dependent boundary conditions.
Linear Algebra and its Applications,
Vol. 503,
Issue. ,
p.
100.
Gao, Chenghua
Ma, Ruyun
and
Zhang, Fei
2017.
Spectrum of discrete left definite Sturm-Liouville problems with eigenparameter-dependent boundary conditions.
Linear and Multilinear Algebra,
Vol. 65,
Issue. 9,
p.
1905.
Aliyev, Ziyatkhan S.
Dunyamaliyeva, Aida A.
and
Mehraliyev, Yashar T.
2017.
Basis Properties in
$${\varvec{L}}_{{\varvec{p}}}$$
L
p
of Root Functions of Sturm–Liouville Problem with Spectral Parameter-Dependent Boundary Conditions.
Mediterranean Journal of Mathematics,
Vol. 14,
Issue. 3,
Aliyev, Ziyatkhan S.
and
Guliyeva, Sevinc B.
2017.
Properties of natural frequencies and harmonic bending vibrations of a rod at one end of which is concentrated inertial load.
Journal of Differential Equations,
Vol. 263,
Issue. 9,
p.
5830.
Gao, Chenghua
Li, Xiaolong
and
Zhang, Fei
2018.
Eigenvalues of discrete Sturm-Liouville problems with nonlinear eigenparameter dependent boundary conditions.
Quaestiones Mathematicae,
Vol. 41,
Issue. 6,
p.
773.
Aliyev, Ziyatkhan S.
and
Namazov, Faiq M.
2019.
On the Spectral Problem Arising in the Mathematical Model of Bending Vibrations of a Homogeneous Rod.
Complex Analysis and Operator Theory,
Vol. 13,
Issue. 8,
p.
3675.
Aliyev, Ziyatkhan S.
and
Mamedova, Gunay T.
2020.
Some properties of eigenfunctions for the equation of vibrating beam with a spectral parameter in the boundary conditions.
Journal of Differential Equations,
Vol. 269,
Issue. 2,
p.
1383.
Möller, Manfred
2020.
Minimality of eigenfunctions and associated functions of ordinary differential operators.
Advances in Operator Theory,
Vol. 5,
Issue. 3,
p.
1014.
Gao, Chenghua
Wang, Yali
and
Lv, Li
2020.
Spectral Properties of Discrete Sturm-Liouville Problems with two Squared Eigenparameter-Dependent Boundary Conditions.
Acta Mathematica Scientia,
Vol. 40,
Issue. 3,
p.
755.
Aliyev, Z. S.
Kerimov, N. B.
and
Mehrabov, V. A.
2020.
Convergence of Eigenfunction Expansions for a Boundary Value Problem with Spectral Parameter in the Boundary Conditions. I.
Differential Equations,
Vol. 56,
Issue. 2,
p.
143.
Aliyev, Ziyatkhan S.
and
Namazov, Faiq M.
2020.
Spectral properties of the equation of a vibrating rod at both ends of which the masses are concentrated.
Banach Journal of Mathematical Analysis,
Vol. 14,
Issue. 2,
p.
585.