No CrossRef data available.
Article contents
Anisotropic weighted isoperimetric inequalities for star-shaped and F-mean convex hypersurface
Published online by Cambridge University Press: 10 February 2025
Abstract
We prove two sharp anisotropic weighted geometric inequalities that hold for star-shaped and F-mean convex hypersurfaces in 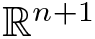 $\mathbb{R}^{n+1}$, which involve the anisotropic p-momentum, the anisotropic perimeter, and the volume of the region enclosed by the hypersurface. We also consider their quantitative versions characterized by asymmetry index and the Hausdorff distance between the hypersurface and a rescaled Wulff shape. As a corollary, we obtain the stability of the Weinstock inequality for the first non-zero Steklov eigenvalue for star-shaped and strictly mean convex domains.
$\mathbb{R}^{n+1}$, which involve the anisotropic p-momentum, the anisotropic perimeter, and the volume of the region enclosed by the hypersurface. We also consider their quantitative versions characterized by asymmetry index and the Hausdorff distance between the hypersurface and a rescaled Wulff shape. As a corollary, we obtain the stability of the Weinstock inequality for the first non-zero Steklov eigenvalue for star-shaped and strictly mean convex domains.
Keywords
MSC classification
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2025. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh



