We consider the parabolic one-dimensional Allen–Cahn equation

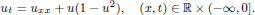
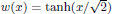The steady state connects, as a ‘transition layer’, the stable phases –1 and +1. We construct a solution u with any given number k of transition layers between –1 and +1. Mainly they consist of k time-travelling copies of w, with each interface diverging as t → –∞. More precisely, we find

where the functions ξj (t) satisfy a first-order Toda-type system. They are given by

for certain explicit constants γjk.