Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Amann, Herbert
and
Escher, Joachim
1996.
Strongly continuous dual semigroups.
Annali di Matematica Pura ed Applicata,
Vol. 171,
Issue. 1,
p.
41.
Angiuli, L.
Pallara, D.
and
Paronetto, F.
2010.
Analytic semigroups generated in L 1(Ω) by second order elliptic operators via duality methods.
Semigroup Forum,
Vol. 80,
Issue. 2,
p.
255.


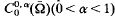 . We also characterise interpolation and extrapolation spaces.
. We also characterise interpolation and extrapolation spaces.