Article contents
Analytic and geometric properties of dislocation singularities
Published online by Cambridge University Press: 01 February 2019
Abstract
This paper deals with the analysis of the singularities arising from the solutions of the problem 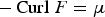 ${-}\,{\rm Curl\ } F=\mu $, where F is a 3 × 3 matrix-valued Lp-function (
${-}\,{\rm Curl\ } F=\mu $, where F is a 3 × 3 matrix-valued Lp-function (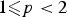 $1\les p<2$) and μ a 3 × 3 matrix-valued Radon measure concentrated in a closed loop in Ω ⊂ ℝ3, or in a network of such loops (as, for instance, dislocation clusters as observed in single crystals). In particular, we study the topological nature of such dislocation singularities. It is shown that
$1\les p<2$) and μ a 3 × 3 matrix-valued Radon measure concentrated in a closed loop in Ω ⊂ ℝ3, or in a network of such loops (as, for instance, dislocation clusters as observed in single crystals). In particular, we study the topological nature of such dislocation singularities. It is shown that 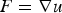 $F=\nabla u$, the absolutely continuous part of the distributional gradient Du of a vector-valued function u of special bounded variation. Furthermore, u can also be seen as a multi-valued field, that is, can be redefined with values in the three-dimensional flat torus 𝕋3 and hence is Sobolev-regular away from the singular loops. We then analyse the graphs of such maps represented as currents in Ω × 𝕋3 and show that their boundaries can be written in term of the measure μ. Readapting some well-known results for Cartesian currents, we recover closure and compactness properties of the class of maps with bounded curl concentrated on dislocation networks. In the spirit of previous work, we finally give some examples of variational problems where such results provide existence of solutions.
$F=\nabla u$, the absolutely continuous part of the distributional gradient Du of a vector-valued function u of special bounded variation. Furthermore, u can also be seen as a multi-valued field, that is, can be redefined with values in the three-dimensional flat torus 𝕋3 and hence is Sobolev-regular away from the singular loops. We then analyse the graphs of such maps represented as currents in Ω × 𝕋3 and show that their boundaries can be written in term of the measure μ. Readapting some well-known results for Cartesian currents, we recover closure and compactness properties of the class of maps with bounded curl concentrated on dislocation networks. In the spirit of previous work, we finally give some examples of variational problems where such results provide existence of solutions.
Keywords
MSC classification
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 150 , Issue 4 , August 2020 , pp. 1609 - 1651
- Copyright
- Copyright © Royal Society of Edinburgh 2019
References
- 5
- Cited by



