Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-18T00:14:38.194Z Has data issue: false hasContentIssue false
  • English
  • Français

Analogues of the bicyclic semigroup in simple semigroups without idempotents

Published online by Cambridge University Press:  14 November 2011

Peter R. Jones
Peter R. Jones
Affiliation:
Department of Mathematics, Statistics and Computer Science, Marquette University, Milwaukee, Wisconsin 53233, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Synopsis

By an important theorem of Andersen, any semigroup, containing idempotents, which is simple but not completely simple contains a copy of the bicyclic semigroup B = 〈a, b | ab = 1〉. In this paper the semigroups A = 〈a, b | a2b = a〉 and C = 〈a, b | a2b = a, ab2 = b〉 are shown to play a similar role in various classes of simple semigroups without idempotents, particularly in those for which Green's relation 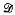is nontrivial. For example it is shown that every right simple semigroup without idempotents is a union of copies of A; every finitely generated simple semigroup without idempotents contains either A or C. In a generalisation of a different sort it is shown that the bicyclic semigroup divides every simple semigroup without idempotents.

Similar results are obtained for 0-simple semigroups without nonzero idempotents.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 106 , Issue 1-2 , 1987 , pp. 11 - 24
Copyright
Copyright © Royal Society of Edinburgh 1987

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Andersen, O.. Ein Bericht über die Struktur abstrakter Halbgruppen (Thesis (Staatsexamensarbeit), Hamburg, 1952).Google Scholar
2Byleen, K.. Embedding any countable semigroup in a 2-generated bisimple monoid. Glasgow Math. J. 25 (1984), 153–161.CrossRefGoogle Scholar
3Byleen, K.. Embedding any countable semigroup without idempotents in a 2-generated simple semigroup without idempotents.Google Scholar
4Clifford, A. H. and Preston, G. B.. The Algebraic Theory of Semigroups (Providence, R.I: American Mathematical Society, 1967).Google Scholar
5Jones, P. R.. Semigroups embeddable in D-trivial semigroups. Semigroup Forum 33 (1986), 441–445.Google Scholar
6McAlister, D. B.. A homomorphism theorem for semigroups. J. London Math. Soc. 43 (1968), 355–366.Google Scholar
7Megyesi, L. and Pollák, G.. On simple principal ideal semigroups. Studia Sci. Math. Hungar. 16 (1981), 437–448.Google Scholar
8Rankin, S. A. and Reis, C. M.. Semigroups with quasi-zeroes. Canad. J. Math. 32 (1980), 511–530.Google Scholar
9Rédei, L.. Halbgruppen und Ringe mit Linkseinheiten ohne Linkseinselemente. Acta Math. Acad. Sci. Hungar. 11 (1960), 217–222.Google Scholar
10Trotter, P. G.. Cancellative simple semigroups and groups. Semigroup Forum 14 (1977), 189–198.Google Scholar