Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-19T22:08:40.425Z Has data issue: false hasContentIssue false
  • English
  • Français

An elliptic boundary-value problem with a discontinuous nonlinearity

Published online by Cambridge University Press:  14 November 2011

G. Keady
G. Keady
Affiliation:
Mathematics Department, University of Western Australia
Get access Rights & Permissions [Opens in a new window]

Synopsis

We study the boundary-value problem, for (λ/k,ψ),

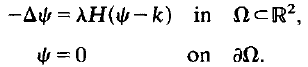
Here ∆ denotes the Laplacian, H is the Heaviside step function and one of A or k is a given positive constant. We define

and usually omit the subscript. Throughout we are interested in solutions with ψ>0 in Ω and hence with λ/=0.

In the special case Ω = B(0, R), denoting the explicit exact solutions by ℑe, the following statements are true, (a) The set Aψ, issimply-connected, (b) Along ℑe, the diameter of Aψ tendsto zero when the area of Aψ, tends to zero.

For doubly-symmetrised solutions in domains Ω such as rectangles, it is shown that the statements (a) and (b) above remain true.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 91 , Issue 1-2 , 1981 , pp. 161 - 174
Copyright
Copyright © Royal Society of Edinburgh 1981

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Alexander, R.. A discontinuous nonlinear eigenvalue problem involving a free boundary. A.M.S. meeting, Knoxville, Nov. 14–15, 1980.Google Scholar
2Benjamin, T. B.. The alliance of practical and analytical insights into the nonlinear problems of fluid mechanics. In Applications of methods of functional analysis to problems in mechanics, Symposium IUTAM/IMU Marseille, Sept. 1975 (eds Germain, P. and Nayroles, B.) Lecture Notes in Mathematics 503, pp. 8–29 (Berlin: Springer, 1976).Google Scholar
3Berger, M. S. and Fraenkel, L. E.. Nonlinear desingularization in certain free-boundary problems. Comm. Math. Phys. 77 (1980), 149–172.CrossRefGoogle Scholar
4Burbea, J.. Vortex motions and conformal mappings. In Nonlinear evolution equations and dynamical systems (eds Bouti, M. et al. ) (Berlin: Springer, 1980).Google Scholar
5Caffarelli, L. A. and Friedman, A.. Asymptotic estimates for the plasma problem. DukeMath. J. 47 (1980), 705–762.Google Scholar
6Crooke, P. S. and Sperb, R. P.. Isoperimetric inequalities in a class of nonlinear eigenvalue problems. SIAM J. Math. Anal. 9 (1978), 671–681.CrossRefGoogle Scholar
7Fraenkel, L. E. and Berger, M. S.. A global theory of steady vortex rings in an ideal fluid. Acta Math. 132 (1974), 13–51.CrossRefGoogle Scholar
8Fraenkel, L. E.. On steady vortex rings of small cross-section in an ideal fluid. Proc. Roy. Soc. London Ser. A 316 (1970), 29–62.Google Scholar
9Fraenkel, L. E.. A lower bound for electrostatic capacity in the plane. Proc. Roy. Soc. Edinburgh Sect. A 88 (1981), 267–273.CrossRefGoogle Scholar
10Friedman, A. and Turkington, B.. Vortex rings: existence and asymptotic estimates. Trans. Amer. Math. Soc. (1981), to appear.CrossRefGoogle Scholar
11Gidas, B., Ni, W. and Nirenberg, L.. Symmetry via the maximum principle. Comm. Math. Phys. 68 (1979), 209–243.CrossRefGoogle Scholar
12Keady, G. and Norbury, J.. A semilinear elliptic eigenvalue problem, II. The plasma problem. Proc. Roy. Soc. Edinburgh Sect. A 87 (1980), 83–109.CrossRefGoogle Scholar
13Lichtenstein, L.. Über einige Existenzprobleme der Hydrodynamik. Math. Z. 23 (1925), 89–154.CrossRefGoogle Scholar
14Lichtenstein, L.. Grundlagen der Hydrodynamik (Berlin: Springer, 1929).Google Scholar
15Moore, D. W. and Saffman, P. G.. Structure of a line vortex in an imposed strain. In Aircraft wake turbulence (eds Olsen, J., Goldburg, A. and Rogers, M.), pp. 339–354 (New York: Plenum Press, 1971).CrossRefGoogle Scholar
16Moore, D. W. and Saffman, P. G.. The density of organized vortices in a turbulent mixing layer. J. Fluid Mech. 69 (1975), 465–473.CrossRefGoogle Scholar
17Norbury, J.. Steady vortex pairs in an ideal fluid. Comm. Pure Appl. Math. 28 (1975), 679–700.CrossRefGoogle Scholar
18Osserman, R.. The isoperimetric inequality. Bull. Amer. Math. Soc. 84 (1978), 1182–1238.CrossRefGoogle Scholar
19Payne, L. E.. Isoperimetric inequalities and their application. SIAM Rev. 9 (1967), 453–488.CrossRefGoogle Scholar
20Payne, L. E.. Bounds for the maximum stress in the Saint-Venant torsion problem. Indian J. Mech. Math. (Special Issue) (1968), 51–59.Google Scholar
21Pierrehumbert, R. T.. A family of steady, translating vortex pairs with distributed vorticity. J. Fluid Mech. 99 (1980), 129–144.CrossRefGoogle Scholar
22Pierrehumbert, R. T. and Widnall, S. E.. The structure of vortices in a free shear layer. J. Fluid Mech. 102 (1981), 301–313.CrossRefGoogle Scholar
23Polya, G. and Szego, G.. Isoperimetric inequalities in mathematical physics (Princeton Univ. Press, 1951).Google Scholar
24Saffman, P. G.. The approach of a vortex pair to a plane surface in inviscid fluid. J. Fluid Mech. 92 (1979), 497–503.CrossRefGoogle Scholar
25Schaefer, P. W. and Sperb, R. P.. Maximum principles and bounds in some inhomogeneous elliptic boundary-value problems. SIAM J. Math. Anal. 8 (1977), 871–878.CrossRefGoogle Scholar
26Schaeffer, D. G.. Nonuniqueness in the equilibrium shape of a confined plasma. Comm. Partial Differential Equations 2 (1977), 587–599.CrossRefGoogle Scholar
27Stakgold, I.. Estimates for certain free boundary problems. In Ordinary and partialdifferential equations, Dundee conference 1980 (eds Everitt, W. N. and Sleeman, B. D.) Lecture Notes in Mathematics 846 (Berlin: Springer, 1981).Google Scholar