Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Tienari, Matti
2000.
Ljusternik–Schnirelmann Theorem for the Generalized Laplacian.
Journal of Differential Equations,
Vol. 161,
Issue. 1,
p.
174.
Le, Vy Khoi
2004.
Generic existence result for an eigenvalue problem with rapidly growing principal operator.
ESAIM: Control, Optimisation and Calculus of Variations,
Vol. 10,
Issue. 4,
p.
677.
Rudd, Matthew
2005.
A direct approach to Orlicz–Sobolev capacity.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 60,
Issue. 1,
p.
129.
DINCA, GEORGE
and
MATEI, PAVEL
2005.
AN EIGENVALUE PROBLEM FOR A CLASS OF NONLINEAR ELLIPTIC OPERATORS.
Analysis and Applications,
Vol. 03,
Issue. 01,
p.
27.
Huentutripay, Jorge
and
Manásevich, Raúl
2006.
Nonlinear Eigenvalues for a Quasilinear Elliptic System in Orlicz–Sobolev Spaces.
Journal of Dynamics and Differential Equations,
Vol. 18,
Issue. 4,
p.
901.
Cianchi, Andrea
2008.
Orlicz-Sobolev Algebras.
Potential Analysis,
Vol. 28,
Issue. 4,
p.
379.
Le, Vy Khoi
2009.
Some existence results and properties of solutions in quasilinear variational inequalities with general growths.
Differential Equations and Dynamical Systems,
Vol. 17,
Issue. 4,
p.
343.
Montenegro, Marcelo
and
Lorca, Sebastián
2012.
The eigenvalue problem for quasilinear elliptic operators with general growth.
Applied Mathematics Letters,
Vol. 25,
Issue. 7,
p.
1045.
Pinasco, Juan Pablo
2013.
Lyapunov-type Inequalities.
p.
1.
Pinasco, Juan Pablo
2013.
Lyapunov-type Inequalities.
p.
85.
Bocea, Marian
and
Mihăilescu, Mihai
2018.
Minimization problems for inhomogeneous Rayleigh quotients.
Communications in Contemporary Mathematics,
Vol. 20,
Issue. 07,
p.
1750074.
Alves, Claudianor O.
Silva, Edcarlos D.
and
Pimenta, Marcos T. O.
2019.
Existence of solution for a class of quasilinear elliptic problem without Δ2-condition.
Analysis and Applications,
Vol. 17,
Issue. 04,
p.
665.
Alberico, A.
di Blasio, G.
and
Feo, F.
2020.
An eigenvalue problem for the anisotropic Φ-Laplacian.
Journal of Differential Equations,
Vol. 269,
Issue. 6,
p.
4853.
Salort, Ariel M.
2020.
Eigenvalues and minimizers for a non-standard growth non-local operator.
Journal of Differential Equations,
Vol. 268,
Issue. 9,
p.
5413.
Santos, Jefferson Abrantes
and
Soares, Sergio H. Monari
2020.
Optimal design problems for a degenerate operator in Orlicz–Sobolev spaces.
Calculus of Variations and Partial Differential Equations,
Vol. 59,
Issue. 6,
Khaled, Mohammed
Rhoudaf, Mohamed
and
Sabiki, Hajar
2020.
Lagrange Multiplier Rule to a Nonlinear Eigenvalue Problem in Musielak–Orlicz Spaces.
Numerical Functional Analysis and Optimization,
Vol. 41,
Issue. 2,
p.
134.
Youssfi, Ahmed
and
Khatri, Mohamed Mahmoud Ould
2020.
On a nonlinear eigenvalue problem for generalized Laplacian in Orlicz–Sobolev spaces.
Nonlinear Analysis,
Vol. 190,
Issue. ,
p.
111607.
Azroul, Elhoussine
Benkirane, Abdelmoujib
and
Srati, Mohammed
2021.
Eigenvalue problem associated with nonhomogeneous integro-differential operators .
Journal of Elliptic and Parabolic Equations,
Vol. 7,
Issue. 1,
p.
47.
Salort, Ariel
and
Vivas, Hernán
2022.
Fractional eigenvalues in Orlicz spaces with no Δ2 condition.
Journal of Differential Equations,
Vol. 327,
Issue. ,
p.
166.
Bahrouni, Sabri
Ounaies, Hichem
and
Salort, Ariel
2023.
Variational eigenvalues of the fractional g-Laplacian.
Complex Variables and Elliptic Equations,
Vol. 68,
Issue. 6,
p.
1021.
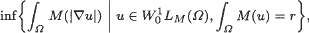
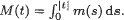 Moreover, the function ur is a weak solution to the corresponding Euler–Lagrange equation
Moreover, the function ur is a weak solution to the corresponding Euler–Lagrange equation