Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-26T02:00:34.198Z Has data issue: false hasContentIssue false
  • English
  • Français

An analytical study of bifurcation problems for equations involving Fredholm mappings

Published online by Cambridge University Press:  14 November 2011

N.X. Tan
N.X. Tan
Affiliation:
Karl-Weierstraß-Institut für Mathematik der Akademie der Wissenschaften der DDR, Mohrenstraße 39, 1086 Berlin, DDR Institute of Mathematics, Hanoi Vietnam Box 631, Buu Dien BO HO, Hanoi, Vietnam
Get access Rights & Permissions [Opens in a new window]

Extract

Let us consider equations in the form

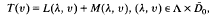
where Λ is an open subset of a normed space. For any fixed λ ∊ Λ, T, L(λ,.) and M(λ,.) are mappings from the closure D0 of a neighbourhood D0 of the origin in a Banach space X into another Banach space Y with T(0) = L(λ, 0) = M(λ, 0) = 0. Let λ be a characteristic value of the pair (T, L) such that T − L(λ,.) is a Fredholm mapping with nullity p and index s, p> s≧ 0. Under sufficient hypotheses on T, L and M, (λ, 0) is a bifurcation point of the above equations. Some well-known results obtained by Crandall and Rabinowitz [2], McLeod and Sattinger [5] and others will be generalised. The results in this paper are extensions of the results obtained by the author in [7].

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 110 , Issue 3-4 , 1988 , pp. 199 - 225
Copyright
Copyright © Royal Society of Edinburgh 1988

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Buchner, M., Marsden, J. and Schecter, S.. Applications of the blowing-up construction and algebraic geometry to bifurcation problems. J. Differential Equations 48 (1983), 404–433.CrossRefGoogle Scholar
2Crandall, M. and Rabinowitz, P.. Bifurcation at simple eigenvalues. J. Fund. Anal. 8 (1971), 321–340.CrossRefGoogle Scholar
3Dancer, E. N.. Bifurcation theory in real Banach spaces. Proc. London Math. Soc. 23 (1971), 699–734.CrossRefGoogle Scholar
4Kluge, R.. Zur Lösung eines Bifurkationsproblems für die Karmanschen Gleichungen im Fall der rechteckigen Platte. Math. Nachr. 44 (1970), 29–54.CrossRefGoogle Scholar
5McLeod, J. B. and Sattinger, D. H.. Loss of stability and bifurcation at a double eigenvalue. J. Fund. Anal. 14 (1973), 62–84.CrossRefGoogle Scholar
6Nirenberg, L.. Topics in nonlinear analysis, Courant Institute Lecture Notes (New York: Courant Institute, 1974).Google Scholar
7Tan, N. X.. An analytical approach to bifurcation problems with applications to partial differential equations. Math. Nachr. 131 (1987), 251–285.CrossRefGoogle Scholar
8Weinberg, M. M. and Trenogin, W. A.. Theorie der Lösungsverzweigung bei nichtlinearen Gleichungen (Berlin: Akademie, 1973).Google Scholar