Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-18T03:20:50.974Z Has data issue: false hasContentIssue false
  • English
  • Français

6.—On the Distribution of the Eigenvalues and the Order of the Eigenfunctions of a Fourth-order Singular Boundary Value Problem

Published online by Cambridge University Press:  14 February 2012

Jyoti Chaudhuri  and
W. N. Everitt
Jyoti Chaudhuri
Affiliation:
Department of Mathematics, Indian Institute of Technology, Madras
W. N. Everitt
Affiliation:
Department of Mathematics, University of Dundee
Get access Rights & Permissions [Opens in a new window]

Synopsis

This paper is concerned with the asymptotic properties of the eigenvalues and eigenfunctions of the boundary value problem

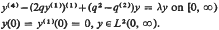
With suitable restrictions placed on the real-valued coefficient q the spectrum of this problem, with respect to the eigenvalue parameter λ, is discrete; let {λn; n = 1, 2, …} and {ψn; n = 1, 2, …} be the eigenvalues and associated eigenfunctions. Asymptotic formulae are obtained for N(λ), the number of eigenvalues not exceeding the real number λ, and for ψn(x) as n→∞ where x is a fixed, positive real number.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 71 , Issue 1 , 1972 , pp. 61 - 75
Copyright
Copyright © Royal Society of Edinburgh 1972

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

References to Literature

[1]Erdélyi, A. et al., 1953. Higher Transcendental Functions, vol. 2. New York: McGraw Hill.Google Scholar
[2]Everitt, W. N., 1963. Fourth order singular differential equations, Math. Annln, 149, 320–340.CrossRefGoogle Scholar
[3]Everitt, W. N., 1968. Some positive definite differential operators, J. Lond. Math. Soc., 43, 465–473.CrossRefGoogle Scholar
[4]Hartman, P., 1951. On the eigenvalues of differential equations, Am. J. Math., 73, 657–662.CrossRefGoogle Scholar
[5]Hartman, P., 1952. On the zeros of solutions of second order linear differential equations, J. Lond. Math. Soc., 27, 492–496.CrossRefGoogle Scholar
[6]Kodaira, K., 1949. The eigenvalue problem for ordinary differential equations of the second order and Heisenberg's theory of S-matrices, Am. J. Math., 71, 921–945.CrossRefGoogle Scholar
[7]Naimark, M. A., 1968. Linear Differential Operators, Part II. New York: Ungar. (German edition, 1960. Berlin: Akademie-Verlag.)Google Scholar
[8]Titchmarsh, E. C., 1939. Theory of Functions, 2nd edn. O.U.P.Google Scholar
[9]Titchmarsh, E. C., 1958 and 1962. Eigenfunction Expansions associated with Second Order Differential Equations. Part I, 2nd edn., 1962. Part II, 1958. O.U.P.CrossRefGoogle Scholar
[10]Titchmarsh, E. C., 1945. On expansion in eigenfunctions, VII, Q. Jl. Math., 16, 103–114.CrossRefGoogle Scholar
[11]Chaudhuri, Jyoti and Everitt, W. N., 1969. On the square of a formally self-adjoint differential expression, J. Lond. Math. Soc., 1, 661–673.CrossRefGoogle Scholar
[12]Chaudhuri, Jyoti and Everitt, W. N., 1969. The spectrum of a fourth-order differential operator, Proc. Roy. Soc. Edinb., 68A, 185–210.Google Scholar