Published online by Cambridge University Press: 14 February 2012
The principal results of this paper concern the spectral properties of the maximal realisation Pp in Lp(Rn) of a formally self adjoint constant coefficient strongly elliptic partial differential operator P(D), assumed to be homogeneous of order 2m, for 1 ≦ p ≦ ∞ and n ≧ 2. If we assume that 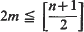 , for 2n/n + l ≦ p ≦ 2n/n−1, together with certain assumptions on the associated real zero surfaces P(ξ) = λ, λ > 0, then σ(Pp) = σc(Pp) = [0, ∞). We obtain an estimate on the norm of the resolvent of Pp for points near the real axis, which allows us to establish the existence of a generalised resolution of the identity in the sense of Kocan.
, for 2n/n + l ≦ p ≦ 2n/n−1, together with certain assumptions on the associated real zero surfaces P(ξ) = λ, λ > 0, then σ(Pp) = σc(Pp) = [0, ∞). We obtain an estimate on the norm of the resolvent of Pp for points near the real axis, which allows us to establish the existence of a generalised resolution of the identity in the sense of Kocan.