Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-23T14:27:10.325Z Has data issue: false hasContentIssue false
  • English
  • Français

2-dimensional Coxeter groups are biautomatic

Part of: Special aspects of infinite or finite groups

Published online by Cambridge University Press:  23 March 2021

Zachary Munro ,
Damian Osajda  and
Piotr Przytycki
Zachary Munro
Affiliation:
Department of Mathematics and Statistics, McGill University, Burnside Hall, 805 Sherbrooke Street West, Montreal, QC, H3A 0B9, Canada ([email protected])
Damian Osajda
Affiliation:
Instytut Matematyczny, Uniwersytet Wrocławski, pl. Grunwaldzki 2/4, 50–384, Wrocław, Poland Institute of Mathematics, Polish Academy of Sciences, Śniadeckich 8, 00-656, Warszawa, Poland ([email protected])
Piotr Przytycki
Affiliation:
Department of Mathematics and Statistics, McGill University, Burnside Hall, 805 Sherbrooke Street West, Montreal, QC, H3A 0B9, Canada ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Let W be a 2-dimensional Coxeter group, that is, one with 1/mst + 1/msr + 1/mtr ≤ 1 for all triples of distinct s, t, r ∈ S. We prove that W is biautomatic. We do it by showing that a natural geodesic language is regular (for arbitrary W), and satisfies the fellow traveller property. As a consequence, by the work of Jacek Świątkowski, groups acting properly and cocompactly on buildings of type W are also biautomatic. We also show that the fellow traveller property for the natural language fails for 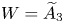$W=\widetilde {A}_3$.

Keywords

Coxeter groupbuildingbiautomatic

MSC classification

Primary: 20F55: Reflection and Coxeter groups
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 152 , Issue 2 , April 2022 , pp. 382 - 401
Check for updates
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

Partially supported by NSERC and AMS.

*

Partially supported by (Polish) Narodowe Centrum Nauki, UMO-2018/30/M/ST1/00668.

References

Bahls, P.. Some new biautomatic Coxeter groups. J. Algebra 296 (2006), 339–347.CrossRefGoogle Scholar
Bridson, M. R. and Haefliger, A.. Metric spaces of non-positive curvature, Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], vol. 319, (Berlin: Springer-Verlag, 1999).CrossRefGoogle Scholar
Brink, B. and Howlett, R. B.. A finiteness property and an automatic structure for Coxeter groups. Math. Ann. 296 (1993), 179–190.CrossRefGoogle Scholar
Caprace, P.-E.. Buildings with isolated subspaces and relatively hyperbolic Coxeter groups. Innov. Incidence Geom. 10 (2009), 15–31.CrossRefGoogle Scholar
Caprace, P.-E. and Mühlherr, B.. Reflection triangles in Coxeter groups and biautomaticity. J. Group Theory 8 (2005), 467–489.CrossRefGoogle Scholar
Cartwright, D. I. and Shapiro, M.. Hyperbolic buildings, affine buildings, and automatic groups. Michigan Math. J. 42 (1995), 511–523.CrossRefGoogle Scholar
Epstein, D. B. A., Cannon, J. W., Holt, D. F., Levy, S. V. F., Paterson, M. S. and Thurston, W. P.. ‘Word processing in groups’ (Boston, MA: Jones and Bartlett Publishers, 1992).CrossRefGoogle Scholar
Farb, B., Hruska, C. and Thomas, A.. Problems on automorphism groups of nonpositively curved polyhedral complexes and their lattices’. Geometry, rigidity, and group actions, Chicago Lectures in Math., Univ. (Chicago, IL: Chicago Press, 2011), 515–560.Google Scholar
Gersten, S. M. and Short, H.. Small cancellation theory and automatic groups. Invent. Math. 102 (1990), 305–334.CrossRefGoogle Scholar
Gersten, S. M. and Short, H.. Small cancellation theory and automatic groups: Part II. Invent. Math. 105 (1991), 641–662.CrossRefGoogle Scholar
Leary, I. and Minasyan, A.. Commensurating HNN-extensions: non-positive curvature and biautomaticity. Geom. Topol., (2020), arXiv:1907.03515, to appear.Google Scholar
Lyndon, R. C. and Schupp, P. E.. Combinatorial group theory’ Ergebnisse der Mathematik und ihrer Grenzgebiete, Band 89, (Berlin-New York: Springer-Verlag, 1977), xiv+339.Google Scholar
Munro, Z.. Weak modularity and $\tilde {A}_n$ buildings. submitted, (2019), arXiv:1906.10259.Google Scholar
Niblo, G. A. and Reeves, L. D.. The geometry of cube complexes and the complexity of their fundamental groups. Topology 37 (1998), 621–633.CrossRefGoogle Scholar
Niblo, G. A. and Reeves, L. D.. Coxeter groups act on CAT(0) cube complexes. J. Group Theory 6 (2003), 399–413.CrossRefGoogle Scholar
Noskov, G. A.. Combing Euclidean buildings. Geom. Topol. 4 (2000), 85–116.CrossRefGoogle Scholar
Ronan, M.. Lectures on buildings, Perspectives in Mathematics, vol. 7, (Boston, MA: Academic Press Inc., 1989), xiv+201.Google Scholar
Świątkowski, J.. Regular path systems and (bi)automatic groups. Geom. Dedicata 118 (2006), 23–48.CrossRefGoogle Scholar