Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-30T23:16:17.627Z Has data issue: false hasContentIssue false
  • English
  • Français

1.—An Algorithm for the Construction of Limit Circle Expressions*†

Published online by Cambridge University Press:  14 February 2012

Anton Zettl
Anton Zettl
Affiliation:
Department of Mathematics, University of Dundee and Northern Illinois University, De Kalb.
Get access Rights & Permissions [Opens in a new window]

Synopsis

Consider the differential expression

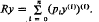
It is shown here that given pn > 0 with pn ∈ C2n(0, ∞) there exist coefficients

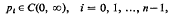
such that all solutions of the equation Ry = 0 are in L2(0,∞). The pi for i<n can be explicitly obtained in terms of pn and a parameter function.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 75 , Issue 1 , 1976 , pp. 1 - 3
Copyright
Copyright © Royal Society of Edinburgh 1976

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Neumark, M. A.. Linear Differentialoperatoren (Berlin: Akademie-Verlag, 1960).CrossRefGoogle Scholar
2Walker, P. W.. Asymptotics for a class of fourth order differential expressions. J. Differential Equations 11 (1972), 321–334.CrossRefGoogle Scholar
3Zettl, A.. The limit point and limit circle cases for polynomials in a differential operator. Proc. Roy. Soc. Edinburgh Sect. A 73 (1975), 301–306.CrossRefGoogle Scholar