Published online by Cambridge University Press: 14 February 2012
The paper gives asymptotic estimates of the form
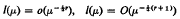
as λ→∞ for the length l(μ)of a gap, centre μ in the essential spectrum associated with second-order singular differential operators. The integer r will be shown to depend on the differentiability properties of the coefficients in the operators and, in fact, r increases with the increasing differentiability of the coefficients. The results extend to all r ≧ – 2 the long-standing ones of Hartman and Putnam [10], who dealt with r = 0, 1, 2.