Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-20T12:43:06.612Z Has data issue: false hasContentIssue false
  • English
  • Français

11.— A Left Definite Multiparameter Eigenvalue Problem in Ordinary Differential Equations*

Published online by Cambridge University Press:  14 February 2012

A. Källström  and
B. D. Sleeman
A. Källström
Affiliation:
Department of Mathematics, University of Dundee.
B. D. Sleeman
Affiliation:
Department of Mathematics, University of Dundee.
Get access Rights & Permissions [Opens in a new window]

Synopsis

The main result of this paper is to establish the completeness of the eigenfunctions for the multiparameter eigenvalue problem defined by the system of ordinary differential equations

0 ≤ x, ≤ 1, r = 1, …, k, subject to the Sturm-Liouville boundary conditions

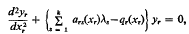
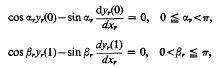
r = 1, …, k. In addition it is assumed that the coefficients ars of the spectral parameters λs, satisfy the ellipticity condition , s = 1, …, k, for all xrɛ[0, 1], r = 1, …, k, and some real k-tuple μ1, …, μk and where 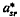is the co-factor of asr in the determinant 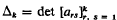. The theory developed here contrasts with the results known when …k is assumed non-vanishing for all xrɛ[0,1].

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 74 , 1976 , pp. 145 - 155
Copyright
Copyright © Royal Society of Edinburgh 1976

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Atkinson, F. V.. Multiparameter eigenvalue problems, 1 (New York: Academic, 1972).Google Scholar
2Browne, P. J.. A multiparameter eigenvalue problem. J Math. Anal. Appl. 38 (1972), 553–568.CrossRefGoogle Scholar
3Faierman, M.. The completeness and expansion theorems associated with the multiparameter eigenvalue problem in ordinary differential equations. J Differential Equations 5 (1969), 179–213.CrossRefGoogle Scholar
4Källström, A. and Sleeman, B. D.. A multiparameter Sturm-Liouville problem. Proceedings of the Conference on the theory of ordinary and partial differential equations. Lecture Notes in Mathematics, 415, 394–401 (Berlin: Springer, 1974).Google Scholar
5Källström, A. and Sleeman, B. D.. An abstract multiparamete eigenvalue problem. Uppsala Univ. Dept Math Rep. 2 (1975).Google Scholar
6Sleeman, B. D.. Multiparameter eigenvalue problems in ordinary differential equations. Bui Inst. Politehn. Iasi 17 (1971), 51–60.Google Scholar
7Sleeman, B. D.. Completeness and expansion theorems for a two-parameter eigenvalue problem in ordinary differential equations using variational principles. J London Math. Soc. 6 (1973), 705–712.CrossRefGoogle Scholar
8Sleeman, B. D.. Singular linear differential operators with many parameters. Proc. Roy. Soc. Edinburgh Sect. A. 71 (1973), 199–232.Google Scholar
9Stummel, F.. Rand und Eigenwertaufgaben in Sobolewschen Räumen. Lecture Notes in Mathematics, 102 (Berlin: Springer, 1969).Google Scholar
10Stummel, F.. Singular Perturbations of elliptic sesquilinear forms. Proceedings of the conference on the theory of ordinary and partial differential equations. Lecture Notes in Mathematics 280, 155–180 (Berlin:Springer, 1972).Google Scholar