Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-12-01T01:19:13.474Z Has data issue: false hasContentIssue false
  • English
  • Français

10.—The Area-function for Non-linear Second-order Oscillations

Published online by Cambridge University Press:  14 February 2012

F. V. Atkinson
F. V. Atkinson
Affiliation:
Department of Mathematics, University of Toronto.
Get access Rights & Permissions [Opens in a new window]

Extract

This paper is concerned with the rate of growth or decline as t → ∞ of oscillatory solutions of equations of the form

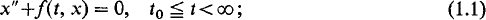
we have in mind equations which resemble in some degree the Lane-Emden-Fowler equation

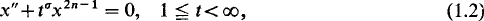
where n ≧ is integral, and σ is either positive, or if negative is not too large, so that oscillatory solutions exist.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 72 , Issue 2 , 1974 , pp. 135 - 147
Copyright
Copyright © Royal Society of Edinburgh 1974

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

References to Literature

[1] Atkinson, F. V., 1954. The asymptotic solution of second-order differential equations. Annali Mat. Pura Appl., 37, 347–378.CrossRefGoogle Scholar
[2] Atkinson, F. V., 1954. On linear perturbation of non-linear differential equations. Can. J. Math., 6, 561–571.CrossRefGoogle Scholar
[3] Atkinson, F. V., 1955. On asymptotically linear second-order oscillations. J. Rat. Mech. Analysis, 4, 769–793.Google Scholar
[4]Atkinson, F. V., 1960. A constant-area principle for steady oscillations. I. J. Math. Analysis Applic., 1, 133–144.CrossRefGoogle Scholar
[5] Bellman, R., 1953. Stability Theory of Differential Equations. New York: McGraw-Hill.Google Scholar
[6] Burton, T. and Grimmer, R. C., 1971. On the asymptotic behaviour of solutions of x″ + a(t)f(x) = 0. Proc. Camb. Phil. Soc. Math. Phys. Sci., 70 77–88.CrossRefGoogle Scholar
[7] Chandrasekhar, S., 1939. Introduction to the Theory of Stellar Structure. Chicago Univ. Press.Google Scholar
[8] Coffman, C. V. and Wong, J. S. W., 1972. Oscillation and non-oscillation of solutions of generalised Emden-Fowler equations. Trans. Am. Math. Soc., 167, 399–434.CrossRefGoogle Scholar
[9] Ehrenfest, P., 1913. A mechanical theorem of Boltzmann and its relation to the theory of energy quanta. K. Ned. Akad. Wet., 16 591–597. (See also Collected Scientific Papers, 1959. Amsterdam: North-Holland.)Google Scholar
[10] Fowler, R. H., 1931. On Emden's and similar differential equations. Q. Jl Math., 2, 259–288.CrossRefGoogle Scholar
[11] Münster, A., 1959. In Enzykl. Phys., 3/2, 244–245. Berlin-Göttingen-Heidelberg: Springer.Google Scholar
[12] Nehari, Z., 1969. A nonlinear oscillation problem. J. Diff. Equations, 5, 452–460.CrossRefGoogle Scholar