This paper, following Stratford [9], considers a boundary layer developing with uniform pressure when x < x0, and with 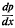large and constant when x > x0. The analysis improves or extends the work of Stratford as follows.

(a) For large values of 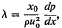inner and outer asymptotic expansions are derived and matched—Stratford considered only the inner solution, his outer boundary condition being determined by physical arguments.

(b) The skin-friction is determined as a series in powers of 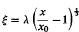, whereas Stratford's, solution was obtained by approximate methods. In the limit as λ→∞ the predicted separation position, ξ = 0.09766, is probably correct to3 significant figures, at least, and differs little from Stratford's value.

(c) This solution further shows that for finite λ, separation occurs when

ξ = 0.09766-0.00014λ−3.

Although the coefficient 0.00014 is not wholly reliable, clearly the position of separation varies little with λ unless λ−3 is very much greater than unity.

(d) The present solution also yields the displacement and momentum thicknesses. When x > x0 the displacement thickness is

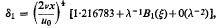
where B1(ξ) is given as a slowly converging seriesin powers of ξ. It is shown how to improve convergence, using certain properties of the flow close to the separation position, and thus to sum the series.

Likewise

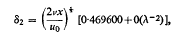
so that when λ is large the momentum thickness changes even less than does the displacement thickness.