Hostname: page-component-745bb68f8f-grxwn Total loading time: 0 Render date: 2025-01-13T09:23:47.008Z Has data issue: false hasContentIssue false
  • English
  • Français

8.—On a Class of Series Expansions in the Theory of Emden's Equation*

Published online by Cambridge University Press:  14 February 2012

Einar Hille
Einar Hille
Affiliation:
Department of Mathematics and Statistics, University of New Mexico, Albuquerque, N.M. 87106, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Synopsis

This paper deals with the nature of movable singularities of solutions of Emden's equation

at which the solution becomes infinite. If m = 1 + 2/p with p > 1 an integer, then the solution becomes infinite at a given point x = c as

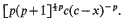
By the general theory of P. Painlevé on movable poles of solutions of non-linear second order differential equations this ‘pseudo-pole’ cannot actually be a pole of order p. Instead of a bona fide Laurent series at x = c we obtain a series expansion of the form

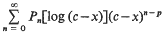
where Pn(t) is a polynomial in t of degree at most [n/(2p + 2)]. The object of this paper is to derive these series and to prove convergence for p = 2. In this case deg [P6m] is strictly equal to m. For other values of p, see Section 8, Addenda.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 71 , Issue 2 , 1973 , pp. 95 - 110
Copyright
Copyright © Royal Society of Edinburgh 1973

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

References to Literature

[1]Emden, R., 1907. Gaskugeln. Anwendungen der mechanischen Wärmetheorie auf Kosmologie und meteorologischen Probleme. Leipzig: Teubner.Google Scholar
[2]Fermi, E., 1927. Un metodo statistico per la determinazione di alcune proprietà dell'atome. Atti Accad. Naz. Lincei Rc. (CI. Sci. Fis. Mat. Nat.) 6, 602–607.Google Scholar
[3]Hille, E., 1969. Lectures on Ordinary Differential Equations. Reading, Mass: Addison-Wesley.Google Scholar
[4]Hille, E., 1969. On the Thomas-Fermi equation. Proc. Natn. Acad. Sci. U.S.A., 62, 7–10.Google Scholar
[5]Hille, E., 1970. Some aspects of the Thomas-Fermi equation. J. Analyse Math., 23, 147–170.Google Scholar
[6]Hille, E., 1970. Aspects of Emden's equation. J. Fac. Sci. Tokyo Univ. (I), 17, 11–30.Google Scholar
[7]Hille, E., 1972. Pseudo-poles in the theory of Emden's equation. Proc. Natn. Acad. Sci. U.S.A., 69, 1271–1272.CrossRefGoogle Scholar
[8]Ince, E. L., 1927 (1944). Ordinary Differential Equations. New York: Dover reprint.Google Scholar
[9]Thomas, L. H., 1927. The calculation of atomic fields. Proc. Camb. Phil. Soc. Math. Phys. Sci., 23, 542–548.Google Scholar
[10]Malmquist, J., 1921. Sur les points singuliers des équations différentielles, I, II. Ark. Mat. Astr. Fys., 15 (3), (27).Google Scholar
[11]Avakumovic, V. G., 1947–1948. Sur l'équation différentielle de Thomas-Fermi I, II. Pubis Inst. Math. Belgr., 1, 101–113; 2, 223–235.Google Scholar
[12]Avakumovic, V. G., 1948. O diferencijalnim jednačinama Thomas-Fermi-eva tipa. Egzistencija integrala. Glas. Srp. Akad. Nauk, 191, 163–185.Google Scholar
[13]Karamata, J., 1947. Sur l'application des théorèmes de nature tauberienne à l'étude des équations différentielles. Pubis Inst. Math. Belgr., 1, 93–97.Google Scholar
[14]Mihailović, M. V., 1950. Sur l'intégrale de l'équation différentielle de Thomas-Fermi autour du point x = 0, y = 1. Pubis Inst. Math. Belgr., 3, 259–270.Google Scholar
[15]Marić, V., 1955. O asimptotskom ponaišanju integrala jadne klase nelinearnih diferencijalnih jednačina drugog reda. Zborn. Rad. Mat. Inst., 4, 27–40.Google Scholar
[16]Karamata, J. and Marić, V., 1960. On some solutions of the differential equation y″(x) = f(x)y λ(x). Rev. Fac. Arts Nat. Sci., Novi Sad, 5, 415–422.Google Scholar