Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-20T12:33:00.984Z Has data issue: false hasContentIssue false
  • English
  • Français

7.—Elliptic Singular Perturbations of First-order Operators with Critical Points

Published online by Cambridge University Press:  14 February 2012

P. P. N. de Groen
P. P. N. de Groen
Affiliation:
Wiskundig Seminarium, Vrije Universiteit, Amsterdam
Get access Rights & Permissions [Opens in a new window]

Synopsis

We study the asymptotic behaviour for ɛ→+0 of the solution Φ of the elliptic boundary value problem

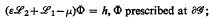
is a bounded domain in ℝ2, 2 is asecond-order uniformly elliptic operator, 1 is a first-order operator, which has critical points in the interior of 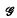, i.e. points at which the coefficients of the first derivatives vanish, ɛ and μ are real parameters and h is a smooth function on 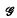. We construct firstorder approximations to Φ for all types of nondegenerate critical points of 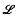1 and prove their validity under some restriction on the range of μ.

In a number of cases we get internal layers of nonuniformity (which extend to the boundary in the saddle-point case) near the critical points; this depends on the position of the characteristics of 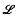1 and their direction. At special values of the parameter μ outside the range in which we could prove validity we observe ‘resonance’, a sudden displacement of boundary layers; these points are connected with the spectrum of the operator ɛ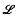2 + 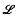1 subject to boundary conditions of Dirichlet type.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 74 , 1976 , pp. 91 - 113
Copyright
Copyright © Royal Society of Edinburgh 1976

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Ackerberg, R. C. and O'Malley, R. E. Jr.Boundary layer problems exhibiting resonance. Stud. Appl. Math. 49 (1970), 277–295.CrossRefGoogle Scholar
2Cook, L. Pamela and Eckhaus, W.. Resonance in a boundary value problem of singular perturbation type. Stud. Appl. Math. 52 (1973), 129–139.CrossRefGoogle Scholar
3Dunford, N. and Schwartz, J. T.. Linear operators, II (New York: Interscience, 1963).Google Scholar
4Eckhaus, W.. Matched asymptotic expansions and singular perturbations. North-Holland Math. Stud. 6 (Amsterdam: North-Holland, 1973).Google Scholar
5Eckhaus, W. and Jager, E. M. de. Asymptotic solutions of singular perturbation problems for linear differential equations of elliptic type. Arch. Rational Mech. Anal. 23 (1966), 26–86.Google Scholar
6Grasman, J.. On the birth of boundary layers. Math. Centrum Amsterdam Tract 36 (1971).Google Scholar
7Groen, P. P. N. de. Critical points of the degenerate operator in elliptic singular perturbation problems. Afd. Zuivere Wisk. Math. Centrum Amsterdam 28 (1975).Google Scholar
8Groen, P. P. N. de. An elliptic boundary value problem with non-differentiable parameters. Arch. Rational Mech and Anal. 42 (1971), 169–183.Google Scholar
9Groen, P. P. N. de. Turning points in second order elliptic singular perturbation problems. Lecture Notes in Math. 280, 273–278 (Berlin: Springer Verlag, 1972).Google Scholar
10Lefschetz, S.. Ordinary differential equations: Geometrical theory(New York: Interscience, 1957).Google Scholar
11Jager, E. M. de. Singular elliptic perturbations of vanishing first order differential operators. Lecture Notes in Math. 280, 73–86 (Berlin: Springer Verlag, 1972).Google Scholar
12Magnus, W., Oberhettinger, F. and Soni, R. P.. Formulas and theorems forthe special functions of mathematical physics (3rd edn). (Berlin: Springer Verlag, 1966).Google Scholar
13Protter, M. H. and Weinberger, H. F.. Maximum principles in differential equations (Englewood Cliffs, N.J.: Prentice-Hall, 1967).Google Scholar
14Sternberg, S.. Local contractions and a theorem of Poincare. Amer. J. Math. 79 (1957), 809–824.CrossRefGoogle Scholar
15van Harten, Aart. Singularly perturbed non-linear 2nd order elliptic boundary value problems (Utrecht Univ. Thesis, 1975).Google Scholar
16Kato, T.. Perturbation theory for linear operators (Berlin: Springer Verlag, 1966).Google Scholar
17Groen, P. P. N. de. Spectral properties of second order singularly perturbed boundary value problems with turning points. J Math. Anal. Appl.to appear. (Preprint—Rep. 39 (1975) Wisk. Sem. Vrije Univ.Amsterdam.)Google Scholar