Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-20T12:33:29.389Z Has data issue: false hasContentIssue false
  • English
  • Français

6.—Rationally Convex Hulls and Potential Theory.*

Published online by Cambridge University Press:  14 February 2012

Richard F. Basener
Richard F. Basener
Affiliation:
Department of Mathematics, Yale University.
Get access Rights & Permissions [Opens in a new window]

Synopsis

Let S be a compact subset of the open unit disc in C. Associate to S the set

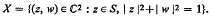
Let R(X) be the uniform algebra on X generated by the rational functions which are holomorphic near X. It is shown that the spectrum of R(X) is determined in a simple wayby the potential-theoretic properties of S. In particular, the spectrum of R(X) is X if and only if the functions harmonic near S are uniformly dense in the continuous functions on S. Similar results can be obtained for other subsets of C2 constructed from compact subsets of C.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 74 , 1976 , pp. 81 - 89
Copyright
Copyright © Royal Society of Edinburgh 1976

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Basener, R.. On rationally convex hulls. Trans. Amer. Math. Soc. 182 (1973), 353–381.CrossRefGoogle Scholar
2Browder, A.. Introduction to function algebras (New York: Benjamin,1969).Google Scholar
3Cole, B.. One-point parts and the peak point conjecture (Yale University: Ph.D. Dissertation, 1968).Google Scholar
4Leeuw, K. de. A type of convexity in the space of n complex variables. Trans. Amer. Math. Soc. 83 (1956), 193–204.Google Scholar
5Leeuw, K. de. Functions on circular subsets of the space of n complex variables. Duke Math. J. 24 (1957), 415–431.CrossRefGoogle Scholar
6Gamelin, T.. Uniform algebras (Englewood Cliffs: Prentice-Hall, 1969).Google Scholar
7Gamelin, T. and Rossi, H.. Jensen measures and algebras of analytic functions. In Function Algebras. Proc. Internat. Sympos. Function Algebras, Tulane University, 1965, pp. 15–35, (Chicago: Scott, Foresman, 1965).Google Scholar
8Gunning, R. and Rossi, H.. Analytic functions of several complex variables (Englewood Cliffs: Prentice-Hall, 1965).Google Scholar
9Helms, L.. Introduction to potential theory (New York: Wiley-Interscience, 1969).Google Scholar
10Huber, A.. Uber Potentiale, welche auf vorgegebenen Mengen verschwinden. Comment. Math Helv. 43 (1968), 51–50.CrossRefGoogle Scholar
11Keldysh, M.. On the solvability and the stability of Dirichlet's problem. Uspekhi Mat. Nauk USSR 8 (1941), 171–231.Google Scholar
12McKissick, R.. A non-trivial normal sup norm algebra. Bull. Amer. Math. Soc. 69 (1963), 391–395.CrossRefGoogle Scholar
13Stout, E.. The theory of uniform algebras (Tarrytown-on-Hudson: Bogden and Quigley, 1971).Google Scholar
14Vladimirov, V.. Methods of the theory of functions of many complex variables (Cambridge, Mass. M.I.T. Press, 1966).Google Scholar
15Wermer, J.. On an example of Stolzenberg. Sympos. Several Complex Variables, Park City, Utah, 1970 Lecture Notes in Math., 184, pp. 79–84 (Berlin: Springer-Verlag, 1971).Google Scholar