Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-26T01:44:10.939Z Has data issue: false hasContentIssue false
  • English
  • Français

26.—The Strong Limit-2 Case of Fourth-order Differential Equations

Published online by Cambridge University Press:  14 February 2012

V. Krishna Kumar
V. Krishna Kumar
Affiliation:
Department of Mathematics, Indian Institute of Technology, Kharagpur, India†
Get access Rights & Permissions [Opens in a new window]

Synopsis

The fourth-order equation considered is

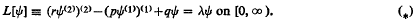
Conditions are given on the coefficients r, p and q which ensure that this differential equation (*) is in the strong limit-2 case at ∞, i.e. is limit-2 at ∞. This implies that (*) has exactly two linearly independent solutions which are in the integrable-square space ℒ2(0, ∞) for all complex numbers λ with im [λ] ≠ 0. Additionally the conditions imply that self-adjoint operators generated by M[·] in ℒ2(0, ∞) are semi-bounded below. The results obtained are applied to the case when the coefficients r, p and q are powers of x ∈ [0, ∞).

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 71 , Issue 4 , 1974 , pp. 297 - 304
Copyright
Copyright © Royal Society of Edinburgh 1974

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

References to Literature

[1]Coddington, E. A. and Levinson, N., 1955. Theory of Ordinary Differential Equations. London and New York: McGraw-Hill.Google Scholar
[2]Eastham, M. S. P., 1971. The limit-2 case of fourth-order differential equations. Q. Jl Math., 22, 131–134.CrossRefGoogle Scholar
[3]Eastham, M. S. P., 1971. On the L 2 classification of fourth-order differential equations. J. Lond. Math. soc., 3, 297–300.CrossRefGoogle Scholar
[4]Everitt, W. N., 1963. Fourth-order singular differential equations. Math. Annln, 149, 320–340.CrossRefGoogle Scholar
[5]Everitt, W. N., 1963. Integrable-square solutions of ordinary differential equations III. Q. Jl Math., 14, 170–180.CrossRefGoogle Scholar
[6]Everitt, W. N., 1968. Some positive definite differential operators. J. Lond. Math. Soc., 43, 465–473.CrossRefGoogle Scholar
[7]Everitt, W. N., 1969. On the limit-point classifications of fourth-order differential equations. J. Lond. Math. Soc., 44, 273–281.CrossRefGoogle Scholar
[8]Everitt, W. N., 1972. On the spectrum of a second order linear differential equation with a p-integrable coefficient. Applicable Analysis, 2, 143–160.CrossRefGoogle Scholar
[9]Everitt, W. N., Giertz, M. and Weidmann, J. J., 1973. Some remarks on a separation and limit-point criterion of second order, ordinary differential expressions Math. Annln 200, 335–346.CrossRefGoogle Scholar
[10]Naimark, M. A., 1968. Linear Differential Operators, II. New York: Ungar.Google Scholar
[11]Walker, P. W., 1971. Asymptotica to the solutions to J. Differential Equations, 9, 108–132.CrossRefGoogle Scholar
[12]Walker, P. W., 1971. Deficiency indices of fourth-order singular differential operators. J. Differential Equations, 9, 133–140.CrossRefGoogle Scholar