Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-19T12:46:37.704Z Has data issue: false hasContentIssue false
  • English
  • Français

17.—An Upper Bound for the Largest Zero of Hermite's Function with Applications to Subharmonic Functions

Published online by Cambridge University Press:  14 February 2012

W. K Hayman  and
E. L Ortiz
Get access Rights & Permissions [Opens in a new window]

Synopsis

Let

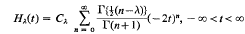
be Hermite's function of order λ and let h = h(λ) be the largest real zero of Hλ(t). Set

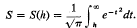
In this paper we establish the inequality

where

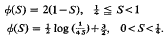
Equality holds for S = ½. The result is also fairly accurate as S→0 and S→1. The proof is analytical except in the ranges −1·1 ≦ h ≦ −0·1 and 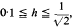where the argument is concluded by means of a computer.

The following deduction is made elsewhere [2, Theorem A]. If u(x) is subharmonic in Rm(m ≧ 2) and the set E where u(x) > 0 has at least k components, where k ≧ 2, then the order ρ of u(x) is at least ϕ(1/k). In particular, if ρ < 1, E is connected. This result fails for ρ = 1.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 75 , Issue 3 , 1976 , pp. 183 - 197
Copyright
Copyright © Royal Society of Edinburgh 1976

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

1Erdélyi, A, Magnus, W, Oberhettinger, F and Tricomi, F. G. Higher Transcendental Functions, I (New York: McGraw-Hill, 1953).Google Scholar
2Friedland, S. and Hayman, W. K.. Eigenvalue inequalities for the Dirichlet problem on spheres and the growth of subharmonic functions. Comment. Math. Helv., to appear.Google Scholar
3Luke, Y. L.. The Special Functions and their Approximation, I and II (New York: Academic Press, 1969).Google Scholar
4Ortiz, E. L.. The Tau Method. SIAM J. Numer. Anal. 6 (1969), 480–492.CrossRefGoogle Scholar
5Ortiz, E. L.. A recursive method for the approximate expansion of functions in a series of polynomials. Comput. Physics Comm. 4 (1972), 151–156.CrossRefGoogle Scholar
6Szegö, G.. Orthogonal polynomials, 3rd edn. Amer. Math. Soc. Colloquium Publications (Providence: Amer. Math. Soc, 1967).Google Scholar
7Wilkinson, J. H.. Rounding Errors in Algebraic Processes (London: H.M.S.O., 1963).Google Scholar