Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-26T01:29:25.189Z Has data issue: false hasContentIssue false
  • English
  • Français

14.—An Example concerning the Separation Property of Differential Operators

Published online by Cambridge University Press:  14 February 2012

W. N. Everitt  and
M. Giertz
W. N. Everitt
Affiliation:
Department of Mathematics, University of Dundee
M. Giertz
Affiliation:
Division of Mathematics, The Royal Institute of Technology, Stockholm, Sweden.
Get access Rights & Permissions [Opens in a new window]

Synopsis

The differential expression M[f] = −f″+qf, on a half-line [a, ∞), is said to be ‘separated’ in L2(a, ∞) if the collection of all functions f ∈ L2(a, ∞) such that M[f] is defined and also in L2(a, ∞), has the property that both terms f″ and qf ar separately in L2(a, ∞). When q is positive and differentiable on [a, ∞) it is known that separation holds for M[·] if q satisfies the condition |q| ≦ 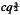on [a, ∞)(*) provided the constant c satisfies 0 < c < 2. This paper constructs a class of examples of the coefficient q to show that (*) does not necessarily yield separation if c > 4/√3>2. The precise upper bound of c for which (*) yields separation is not known.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 71 , Issue 2 , 1973 , pp. 159 - 165
Copyright
Copyright © Royal Society of Edinburgh 1973

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

References to Literature

[1]Atkinson, F. V., 1973. On some results of Everitt and Giertz. Proc. Roy. Soc. Edinb., 71A, 151–158.Google Scholar
[2]Everitt, W. N. and Giertz, M., 1971. Some properties of the domains of certain differential operators. Proc, Lond. Math. Soc., 3, 301–324.CrossRefGoogle Scholar
[3]Everitt, W. N. 1972. Some inequalities associated with certain ordinary differential operators. Math. Z., 126, 308–326.CrossRefGoogle Scholar
[4]Everitt, W. N., Inequalities and separation criteria for certain differential operators (to be published).Google Scholar
[5]Everitt, W. N., Giertz, M. and Weidmann, J. Some remarks on a separation and limit-point criterion of second-order ordinary differential expressions. Math. Annln (in press).Google Scholar
[6]Naimark, M. A., 1968. Linear Differential Operators: Part II. New York: Ungar.Google Scholar
[7]Titchmarsh, E. C., 1962. Eigenfunction expansions associated with second-order differential equations: Part I (2nd edn). O.U.P.CrossRefGoogle Scholar