Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-20T12:26:14.540Z Has data issue: false hasContentIssue false
  • English
  • Français

10.—An Abstract Relation for Multiparameter Eigenvalue Problems*

Published online by Cambridge University Press:  14 February 2012

A. Källström  and
B. D. Sleeman
A. Källström
Affiliation:
Department of Mathematics, University of Dundee.
B. D. Sleeman
Affiliation:
Department of Mathematics, University of Dundee.
Get access Rights & Permissions [Opens in a new window]

Synopsis

Consider the multiparameter system

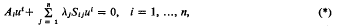
where ut is an element of a separable Hilbert space Hi, i = 1, …, n. The operators Sij are assumed to be bounded symmetric operators in Hi and Ai is assumed self-adjoint. In addition consider the operator equation

where B is densely defined and closed in a separable Hilbert space H and Tj, j = 1, …, n is a bounded operator in H. The problem treated in this paper is to seek an expression for a solution v of (**) in terms of the eigenfunctions of the system (*).

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 74 , 1976 , pp. 135 - 143
Copyright
Copyright © Royal Society of Edinburgh 1976

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Arscott, F. M.. Periodic differential equations (Oxford: Pergamon, 1964).Google Scholar
2Arscott, F. M.. Transform theorems for two-parameter eigenvalue problems in hilbert space. Proceedings of the conference on the theory of ordinary and partial differential equations. Lecture Notes in Mathematics 415, 302–307 (Berlin: Springer, 1974).Google Scholar
3Atkinson, F. V.. Multiparameter eigenvalue problems, 1 (New York: Academic, 1972).Google Scholar
4Browne, P. J.. A multiparameter eigenvalue problem. J Math. Anal. Appl. 38 (1972), 553–568.Google Scholar
5Faierman, M.. The completeness and expansion theorems associated with the multiparameter eigenvalue problem in ordinary differential equations. J.Differential Equations. 5 (1969), 179–213.CrossRefGoogle Scholar
6Ince, E. L.. Ordinary differential equations (New York: Dover, 1956).Google Scholar
7Källström, A. and Sleeman, B. D.. A multiparameter Sturm-Liouville problem. Proceedings of the conference on the theory of ordinary and partial differential equations. Lecture Notes in Mathematics 415, 394–401 (Berlin: Springer 1974).Google Scholar
8Källström, A. and Sleeman, B. D.. An abstract multiparameter eigenvalue problem. Uppsala Univ. Dept Math Rep. 2 (1975).Google Scholar
9Murray, F. J. and Neumann, J. Von. On rings of operators. Ann. of Math. 37 (1936), 116–229.CrossRefGoogle Scholar
10Schatten, R.. A theory of cross-spaces. Ann. of Math. Studies. 26 (1950).Google Scholar
11Sleeman, B. D.. Multiparameter eigenvalue problems in ordinary differential equations. Bui. Inst. Politehn. Iasi 17 (1971), 51–60.Google Scholar
12Sleeman, B. D.. Multiparameter eigenvalue problems and k-linear operators. Proceedings of the conference on the theory of ordinary and partial differential equations. Lecture Notes in Mathematics 280, 347–353 (Berlin: Springer, 1972).Google Scholar
13Sleeman, B. D.. Completeness and expansion theorems for a two-parameter eigenvalue problem in ordinary differential equations using Variational principles. J. London Math. Soc. 6 (1973), 705–712.CrossRefGoogle Scholar
14Sleeman, B. D.. Singular linear differential operators with many parameters. Proc. Roy. Soc. Edinburgh Sect. A. 71 (1973), 199–232.Google Scholar