No CrossRef data available.
Published online by Cambridge University Press: 01 August 2006
We summarize a continuing investigation of turbulence in high-latitude translucent molecular clouds. These low mass (~50–100 M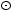 ), nearby (~100 pc), non-star forming clouds appear to be condensing out of the atomic cirrus. Unlike star-forming clouds the velocity fields in the clouds must be driven by external processes. Our detailed mapping of the clouds MBM 3,16 and 40 indicates that the dynamics in these clouds result from the combination of shear-flow and thermal instabilities, not shocks. These clouds also show coherent structures, non-Gaussian PDFs but no clear velocity-size relation. Lastly, the energetics of these clouds indicate that radiative loss may terminate the cascade before local heating takes place.
), nearby (~100 pc), non-star forming clouds appear to be condensing out of the atomic cirrus. Unlike star-forming clouds the velocity fields in the clouds must be driven by external processes. Our detailed mapping of the clouds MBM 3,16 and 40 indicates that the dynamics in these clouds result from the combination of shear-flow and thermal instabilities, not shocks. These clouds also show coherent structures, non-Gaussian PDFs but no clear velocity-size relation. Lastly, the energetics of these clouds indicate that radiative loss may terminate the cascade before local heating takes place.