Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-23T10:41:21.500Z Has data issue: false hasContentIssue false
  • English
  • Français

Solar Surface Anisotropy effect on the Magnetic Field

Published online by Cambridge University Press:  24 July 2015

Véronique Bommier
Véronique Bommier*
Affiliation:
LESIA, Observatoire de Paris, CNRS-INSU-UMR8109, UPMC Univ. Paris 06, Université Paris Diderot-Paris 7; 5, Place Jules Janssen, 92190 Meudon, France
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Within the literature there are at least 15 references indicating that the horizontal magnetic flux does not exactly balance vertical flux in sunspots, leading to the surprising result that div 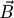$\vec{B}$ would depart from zero. Intuitively, this has to be related to the stratification at the surface of the star, due to which horizontal and vertical typical lengths are different. This surface anisotropy results from gravity, but how does gravity influence the magnetic field? To answer this question, a scenario has been proposed in two recent publications, based on anisotropic Debye shielding. The presentation reported in this paper was devoted to investigate the possibility and causes of a non-zero div 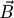$\vec{B}$. A scaling law associated with the anisotropy is able to reestablish the nullity of div 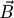$\vec{B}$, which would lead to a renewed MHD in the solar photosphere layer. An eventual observation in the laboratory is also reported.

Keywords

Sun: magnetic fieldsSun: photospheresunspotsMHD
Type
Contributed Papers
Information
Proceedings of the International Astronomical Union , Volume 10 , Symposium S305: Polarimetry: From the Sun to Stars and Stellar Environments , December 2014 , pp. 28 - 34
Copyright
Copyright © International Astronomical Union 2015 

References

Bommier, V. 2013, Physics Research International vol. 2013, Article ID 195403, 16 pages, doi:10.1155/2013/195403, http://www.hindawi.com/journals/physri/2013/195403/ CrossRefGoogle Scholar
Bommier, V. 2014, Comptes Rendus Physique 15, 430 CrossRefGoogle Scholar
Bommier, V., Landi Degl'Innocenti, E., Landolfi, M., & Molodij, G. 2007, A&A 464, 323 Google Scholar
Brethouwer, G., Billant, P., Lindborg, E., & Chomaz, J.-M. 2007, Journal of Fluid Mechanics 585, 343 Google Scholar
Bruhat, G. 1967 Cours de Physique Générale: Électricité, MassonGoogle Scholar
Dirac, P. A. M. 1931, Royal Society of London Proceedings Series A 133, 60 Google Scholar
Faurobert, M., Aime, C., Périni, C., et al. 2009, A&A 507, L29 Google Scholar
Gekelman, W., Pfister, H., Lucky, Z., et al. 1991, Review of Scientific Instruments 62, 2875 Google Scholar
Grec, C., Uitenbroek, H., Faurobert, M., & Aime, C. 2010, A&A 514, A91 Google Scholar
Jackson, J. D. 1975, Classical Electrodynamics, 2nd Edition, Wiley & Sons Google Scholar
Khomenko, E., & Collados, M. 2007, ApJ 659, 1726 Google Scholar
Leka, K. D., Barnes, G., Crouch, A. D., et al. 2009, Solar Phys. 260, 83 Google Scholar
Metcalf, T. R. 1994, Solar Phys. 155, 235 Google Scholar
Meyer-Vernet, N. 1993, American Journal of Physics 61, 249 Google Scholar
Meyer-Vernet, N. 2007, Basics of the Solar Wind, Cambridge University Press, Cambridge CrossRefGoogle Scholar
Puschmann, K. G., Ruiz Cobo, B., & Martínez Pillet, V. 2010, Ap. Lett. 721, L58 Google Scholar
Van Compernolle, B., Bortnik, J., Pribyl, P., et al. 2014, Physical Review Letters 112, 145006 Google Scholar