No CrossRef data available.
Article contents
Mean Velocity of Local Populations: Axiality, Age and Time Dependence
Published online by Cambridge University Press: 01 August 2006
Abstract
The segregated disk populations obtained from applying the MEMPHIS algorithm (Cubarsi & Alcobé, This symposium) to the Hipparcos catalogue are the basis of the following important kinematical results (Cubarsi & Alcobé 2006). In particular, the thick disk population was extrapolated until reaching an asymptotic ideal axisymmetric population. The obtained no net radial motion point had a radial heliocentric velocity of 20 ± 1 Km s−1 toward the galactic anticentre, which is the opposite of the solar radial motion.
According to the obtained population mean velocities, an intriguing question arose: Why the young thin disk population, the continuum of old thin disk stars, and the thick disk, are moving, on average, in the same direction, as belonging to an unique main stream? On the other hand, the early thin disk population, in the region of the Hyades-Pleiades supercluster, remains as an isolated population, with a nearly null radial mean velocity.
The thick disk stars drawn from increasing Hipparcos subsamples showed a decreasing trend of vertex deviation (Cubarsi & Alcobé 2004, Alcobé & Cubarsi 2005), by indicating a clear trend to axial-symmetry. If we assume that the asymptotic thick disk is nearly in steady state, then we can also admit a null radial mean velocity for the oldest thick disk. Thus, in the plane, using galactocentric cylindrical coordinates, with star velocities Π (toward the Galactic anticentre) and Θ (in the rotational direction), the mean velocity of thick disk stars satisfies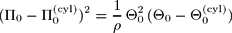 where Π0(cyl) and Θ0(cyl) are the mean velocities of a pure axial population, and ρ is a constant.
where Π0(cyl) and Θ0(cyl) are the mean velocities of a pure axial population, and ρ is a constant.
The rotation mean velocity of such an ideal axial and steady state thick disk was extrapolated for Π0=Π0(cyl)=0, giving a value of Π0(cyl) = 138 ± 2 Km s−1. Moreover, the progressive partial thick disk populations were also extrapolated in the Π Θ plane, up to the above rotation mean velocity, leading to a solar galactocentric radial velocity of Π⊙ = −20 ± 1 Km s−1.
The centroid of such an asymptotic local thick disk (or local halo) is moving on a circular orbit, similarly to the early-thin disk. The young-thin disk is moving on the most eccentric elliptical orbit. This fact would be consistent with the effect of a Galactic bar moving stars from circular to eccentric orbits, in the journey from the early to the young thin disk. As the stars get older, the disk populations partially lose their average angular momentum, as well as they lose radial motion and increase their velocity dispersion.
Finally, let us remark that the mean radial velocity of the thick disk stars remains explained as the addition of a term due to the non axiality of the system, and a term due to the system's time dependence, which is clearly non-null. Both terms are acting in opposite senses, and are more important for younger than for older stars. The term due to the deviation from axial symmetry increases the radial motion toward the Galactic center, while the time dependent term opposes it, in a trend to recover the axial symmetry, that is reached for the extrapolated population.
- Type
- Contributed Papers
- Information
- Proceedings of the International Astronomical Union , Volume 2 , Symposium S235: Galaxy Evolution Across the Hubble Time , August 2006 , pp. 85
- Copyright
- Copyright © International Astronomical Union 2007


